Solution:

Ans. (i) Try yourself similar Q. 5 Long Answer Type Question.

(ii)

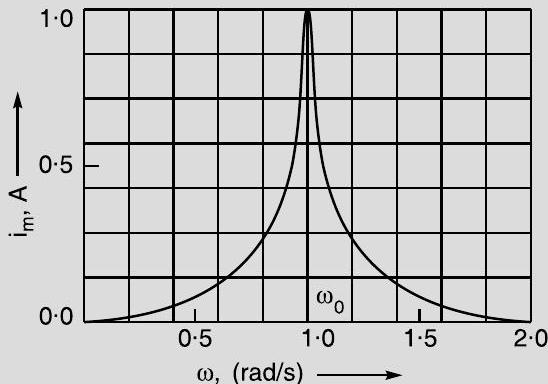
1

The capacitance of a capacitor in the tuning circuit is varied such that the resonant frequency of the circuit becomes nearly equal to the frequency of the radio signal to be received. When this happens, the amplitude of the current becomes maximum in the receiving circuit.

1

[CBSE Marking Scheme 2013]

TOPIC-3

AC Generator and Transformer

Revision Notes

$AC$ generator

• An alternator is an electrical machine which converts mechanical energy into alternating electrical energy.

Alternator or a synchronous generator has a stator and rotor.

• It is similar to the basic working principle of a $dc$ generator.

It works on the principle of electromagnetic induction where a coil gets rotated in uniform magnetic field, sets an induced emf given as :

$$e=e_0\sin \omega t=NBA\omega \sin \omega t$$

Transformer

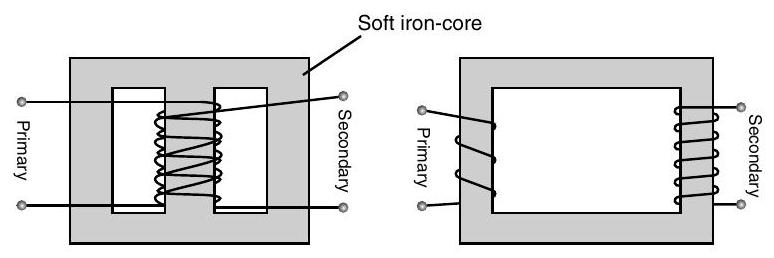
T Transformer is an electrical device used for changing the alternating voltages.

$>$ It is based on the phenomenon of mutual induction.

The main use of transformer is in transmission of $ac$ over long distances at extremely high voltages which reduces the energy losses in transmission.

It comprises of two sets of coils which are insulated from each other and are wound on soft-iron core.

In this, one of the coil is called as primary (input coil) having $N_p$ turns while other coil is secondary (output coil) having $N_s$ turns, so we have

$$\frac{E_s}{E_p}=\frac{I_p}{I_s}=\frac{N_s}{N_p}=k$$

Transformer Ratio :

$$E_s=\left(\frac{N_s}{N_p}\right)E_p\text{ and }{I}_s=\left(\frac{N_p}{N_s}\right)I_p$$

$\frac{N_S}{N_p}=\frac{V_s}{V_p}$ is defined as the transformer ratio.

The value of turns ratio of a transformer $\frac{N_p}{N_s}=\frac{V_p}{V_s}=n$

Step-up transformer : If secondary coil has more number of turns than primary $(N_s>N_p)$, voltage gets stepped up $(V_s>V_p)$.

In this, there is less current in secondary as compared topimary $(\frac{N_s}{N_p}>1$ and $I_s<I_p)$.

The value of transformer ratio

$k>1$

Step-down transformer: In this, the secondary coil has less number of turns than primary $(N_s<N_p)$. In this, $V_s<V_p$ and $I_s>I_p$ as voltage gets stepped down or reduced with increase in current.

In this, value of transformer ratio

$$k<1$$

The main use of transformers is instepping up voltage for power transmission.

• Electric power can be transmitted much more efficiently at high voltages than at low voltages due to less $I^{2}R$ heat loss in a high voltage / low current transmission.

Efficiency of transformer:

$$\begin{array}{rlr}\eta & =\frac{\text{ output power }}{\text{ input power }}\eta & =\frac{E_s{I}_s}{E_p{I}_p}\end{array}$$

Inspite of heavy power losses, the efficiency in a transformer is usually above $90$.

An ideal transformer is $100$ efficient as it delivers all energy it receives.

Real transformer is not $100$ efficient and at full load, its efficiency lies between $94$ to $96$.

• A transformer operating with constant voltage and frequency with very high capacity, efficiency results as $98$.

Energy losses in transformers :

1. Flux Leakage
2. Resistance of windings
3. Eddy currents
4. Hysteresis

Know the Formulae

$>\frac{E_S}{E_p}=\frac{I_p}{I_s}=\frac{N_s}{N_p}=k$ $>V_s=\left(\frac{N_s}{N_p}\right)V_p$ and $I_s=\left(\frac{N_p}{N_s}\right)I_p$

• The value of transformer ratio is greater than 1 for step up transformer and less than 1 for step-down transformer.

$\eta =\frac{E_s{I}_s}{E_p{I}_p}$

$>$ efficiency $=\frac{\text{ Output power }}{\text{ Input power }}\times 100$

$$=\frac{\text{ Input power }-\text{ Losses }}{\text{ Input power }}\times 100$$

$>e=e_0\sin \omega \mathrm{t}=NBA\omega \sin \omega t$

$I=\frac{e}{r}I=\frac{NBA\omega \sin \omega t}{R}$

? Objective Answer Type Questions