alternating-currents Question 18
Question: Q. 2. (i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage?
(ii) Without making any other change, find the value of the additional capacitor $C_{1}$, to be connected in parallel with the capacitor $C$, in order to make the power factor of the circuit unity.
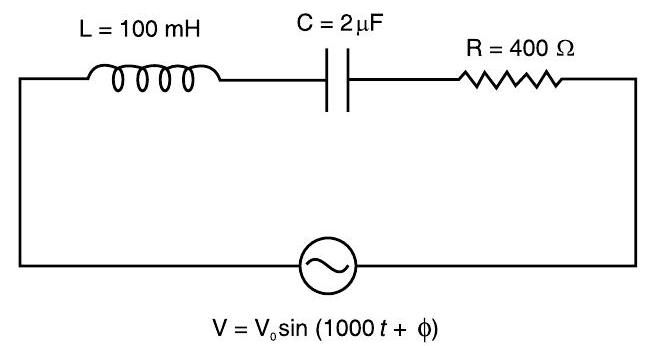
U] [Delhi I, II, III 2017]
Show Answer
Solution:
Ans. (i) Calculation of phase difference between current and voltage
Name of quantity which leads
(ii) Calculation of value of ’ $C$ ‘, is to be connected in parallel
(i) $\quad X_{L}=\omega L=\left(1000 \times 100 \times 10^{-3}\right) \Omega$
$$ =100 \Omega $$
$$ X_{C}=\frac{1}{\omega C}=\left(\frac{1}{1000 \times 2 \times 10^{-6}}\right) \Omega $$
$$ =500 \Omega $$
Phase angle
$$ \begin{aligned} \tan \phi & =\frac{X_{L}-X_{C}}{R} \ \tan \phi & =\frac{100-500}{400}=-1 \ \phi & =-\frac{\pi}{4} \end{aligned} $$
As $X_{C}>X_{L}$ (phase angle is negative), hence current leads voltage (ii) To make power factor unity
$$ \begin{align*} X_{C^{\prime}} & =X_{L} \ \frac{1}{\omega C^{\prime}} & =100 \ C^{\prime} & =10 \mu \mathrm{F} \ C^{\prime} & =C+C_{1} \ 10 & =2+C_{1} \ C_{1} & =8 \mu \mathrm{F} \end{align*} $$
[CBSE Marking Scheme 2017]
[AI Q. 3. A sinusoidal voltage of peak value $10 \mathrm{~V}$ is applied to a series $L C R$ circuit in which resistance, capacitance and inductance have values of $10 \Omega$, $1 \mu \mathrm{F}$ and $1 \mathrm{H}$ respectively. Find (i) the peak voltage across the inductor at resonance (ii) quality factor of the circuit.
U] [CBSE SQP 2018-19]
Ans.
$$ I_{0}=V_{0} / R=10 / 10=1 \mathrm{~A} \quad 1 / 2 $$
$\omega_{r}=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{\left(1 \times 1 \times 10^{-6}\right)}}{ }^{1 / 2}$
$=10^{3} \mathrm{rad} / \mathrm{s}$
$V_{0}=I_{0} X_{L}=I_{0} \omega_{r} L$
$=1 \times 10^{3} \times 1=10^{3} \mathrm{~V}$
$Q=\omega_{r} L / R$
$=\left(10^{3} \times 1\right) / 10=100 \quad 1 / 2$
[CBSE Marking Scheme 2018]
