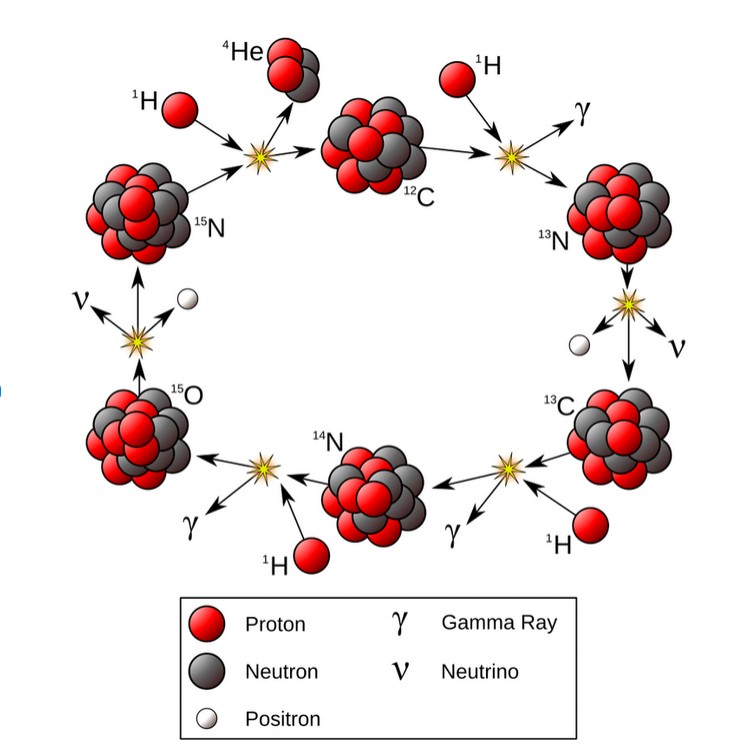
Carbon Cycle

Death of Stars

More on stability

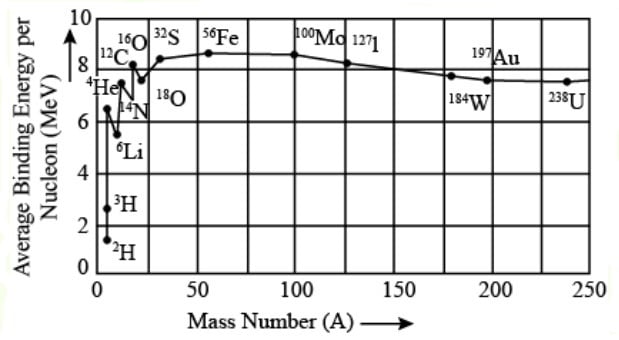
Binding energy per nucleon along the “valley of stability”

More phenomena

• Fission
• Radioactivity
• Gamma decay

Spontaneous fission

Break up into smaller nuclei

Condition: $\frac{Z^2}{A}>47$

Example

$^{235}U \rightarrow {} ^{140}Xe + {} ^{92}Sr + 3n$

$\text {Energy liberated: } 173 ~MeV$

Catch: Probability for decay $\sim 10^{-11}$ per second!

$A \longrightarrow X_1+X_2+H e$

$+n_1 \beta+n_2 \gamma$

$r_1 + r_2 = n_1$

Spontaneous probabilistic process

Beta decay

$\beta^{-} \equiv e^{-} ; \quad \beta^{+} \equiv e^{+}$

$\alpha$ decay (alpha $\left.\equiv{ }^4 \mathrm{He}\right)$

$\gamma$ decay (De-excitation)

Electromagnetic

$\gamma \text { decay }$

De-excitation of Nuclei

Example:

$^{10} {Be}^{\star} \rightarrow ^{10} {Be}+\gamma$

${}_{56}^{137}Ba^{\star} \rightarrow _{56}^{137}Ba + \gamma$

No change in $A, Z$.

$\text {Atoms Hydrogen }$

$n = 3$

$n = 2$

$10.2 \text { ev }$

$n = 1$

$\frac{13.6}{4} = 3.4$

$13.6 - 3.4 = 10.2$

Compound Nucleus

$\alpha - \text {Particle } = {}_2^4 He$

$M ( {} _ {94} ^{240} Pu) \rightarrow M ( {} _ {92} ^{236} U) + M ( {} _ {2} ^{4} He)$

$M_{P U} {^{c^2}}>M_U {^{C^2}}+{M}_{H e} c^2 +$

$\tiny\left[M_P-\left(M_{D_1}+M_{\mathrm{He}}\right)\right] c^2=Q$

$Q- \text {Factor}$

Neutrino Accompaniment

${ }_Z^A \mathrm{X} \rightarrow _{\mathrm{Z}+1}^{\mathrm{A}} \mathrm{Y}+\mathrm{e}^{-}+\bar{V}$

${ }_Z^A \mathrm{X} \rightarrow _{\mathrm{Z}-1}^{\mathrm{A}} \mathrm{Y}+\mathrm{e}^{+}+{V}$

Beta Decay

$\alpha$ decay: the 4 particles $(2 n+2 p)$ were inside the nucleus.

$(2 n+2 p) -$ There is no production as such

Beta decay

${}_z^A X$

$z \rightarrow \text{ Protons }$

$A-z \rightarrow \text{ Neutrons }$

There are no ${\beta^- \text { or } \beta^+}$

$n \longrightarrow p+e^{-}+\bar{\nu}$

$p^* \longrightarrow n+e^{+}+\nu$

$n \rightarrow p+\mathrm{e}^{-}+\bar{v}$

$^{14} {C} \rightarrow^{14} {N}+{e}^{-}+\bar{v}$

$^{10} {C} \rightarrow ^{10} {B}+v+{e}^{+}$

Fundamental Process

$p \longrightarrow n+e^++\nu$

${m_p

Hydrogen is stable

$p^* \rightarrow n+e^{+}+\nu$

Chain reaction

${}_{90}^{232}\text{Th} \rightarrow _{88}^{228}\text{Ra} + _2^4 \text{He}$

${ }_{88}^{228}\mathrm{Ra} \rightarrow _{89}^{228} \mathrm{Ac}+\mathrm{e}^{-}$

${ }_{89}^{228} \mathrm{Ac} \rightarrow _{90}^{228}\mathrm{Th}+\mathrm{e}^{-}$

${ }_{90}^{228} \mathrm{Th} \rightarrow _{88}^{224} \mathrm{Ra}+_2^4 \mathrm{He}$

${\text{Uranium Chain}}$

Credit: Freidlander et al

$\text{Laws of radioactivity}$

Important Features

Law of Large Numbers

Satistical in Nature

Only Probability matters

Gave rise to Quantum Mechanics!

Decay Rate depends on the Population at that Instant

$-R \equiv \frac{\mathrm{dN}(\mathrm{t})}{\mathrm{dt}}$

$=-\lambda N(t) ; \quad \lambda>0$

$R$ is also called activity.

Units of $R$ : Becquerel (SI);

Curie $(\mathrm{Ci})=3.7 \times 10^{10}$ Becquerel

$\frac{d N(t)}{d t}=-\lambda N(t)$

$R(t)\equiv\lambda N(t)$

$R(t) - \text {activity}$

Activity decreases with time

$R\left(t_1\right)=\lambda N\left(t_1\right)$

$R\left(t_2\right)=\lambda N\left(t_2\right)$

$\underline{t_2 >t_1}$

$\frac{R\left(t_2\right)}{R\left(t_1\right)}=\frac{N\left(t_2\right)}{N\left(t_1\right)}< 1$

$-\frac{d N}{d t}=R(t)=\lambda\ \underbrace{N(t)}$

$N(t)\rightarrow \text{ dimension less. }$

$[\lambda] = \frac{1}{T}$

$[R]= \frac{1}{T}$

$[R]= \frac{1}{T} = \text{ S I } (s^{-1})$

$[R]= \frac{1}{T} = \text { Ci }$

$\lambda = \text{SI} (s^{-1}): \text{ Becquerel }$

$\lambda = \text{Ci}\rightarrow \text{ Curie }$

Decay Rate depends on the Population at that Instant

$-R \equiv \frac{\mathrm{dN}(\mathrm{t})}{\mathrm{dt}} =-\lambda N(t) ; \quad \lambda>0$

$R$ is also called activity. Units of $R$ : Becquerel (SI); Curie $(\mathrm{Ci})=3.7 \times 10^{10}$ Becquerel

Half Life and Mean life

$T_{1.2} =\frac{\ln 2}{\lambda} \equiv \frac{0.693}{\lambda}$

$\tau =\frac{1}{\lambda}$

Solution of decay equation

$\frac{d N(t)}{d t} =-\lambda N {(t)}$

$\int_0^t \frac{d N}{N} =-\lambda \int_0 ^td t^{\prime}$

$\ln \frac{N(t)}{N(0)} =-\lambda t \quad \quad \Rightarrow N(t) = N_0 e^{-\lambda t}$

$N_0 e^{-\lambda t}=$ Exponential decay Not a linear decay

$N(t)=N_0 e^{-\lambda t}$

$t=0, N=N_0$

$t=T_{1 / 2} ; N=\frac{N_0}{2}$

$T_{1/2} = \text{ half-life }$

$N\left(T_{1/2}\right) =N_0e ^{-\lambda T_{1/2}}=\frac{N_0}{2}$

$e^{-\lambda T_{1/2}} =\frac{1}{2}$

$\Rightarrow T_{1/2} =\frac{\ln 2}{\lambda}$

$[\therefore \frac{\ln 2}{\lambda} = \text { Natural }]$

When would all the particles decay if the rate were the same at $t=0$ ?

$\overline{N_t}=N_0-\left(\lambda N_0\right) t$

$\text {And }\overline{N}=0 \text { when }$

$t=\frac{1}{\lambda} \equiv \tau$

Radioactivity: meanlife

Extrapolation

Sequential Process

$A_1\left(\lambda_1\right) \rightarrow A_2\left(\lambda_2\right) \rightarrow \cdots A_n$

$\frac{d N_1}{d t}=-\lambda_1 N_1(t)$

$\frac{d N_2}{d t}=\lambda_1 N_1(t)-\lambda_2 N_2(t)$

And so on

Multiple Modes

A given source has multiple decay modes

$d N(t)=-${$\lambda_1+\lambda_2+\cdots \lambda_n$} $N(t) d t$

The ratios $\frac{\lambda_i}{\lambda_j}$ give the relative decay rates for various daughters