mathematics-class-12-unit-13-chapter-04-probability-some-problems-on-probability-l-4-10-r6kzd9gecmu

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-1 </primary>
<hr>
<main>

- 1. Let $A$ and $B$ be any two events with

- $P\left(A^c\right)=0.3, P(B)=0.4, P(A-B)=0.5$. Find $P\left(B \mid A \cup B^C\right)$.

- solution: $\quad P\left(B \mid A \cup B^c\right)=\frac{P\left(B \cap\left(A \cup B^c\right)\right)}{P\left(A \cup B^c\right)}$

- $\text { Numerator: } P\left((B \cap A) \cup\left(B \cap B^C\right)\right)$

- $= P((B \cap A) \cup \phi)=P(A \cap B)$

- $ A=(A-B) \cup(A \cap B)$

- $\Rightarrow P(A)=P(A-B)+P(A \cap B)$

- $\Rightarrow P(A \cap B)=P(A)-P(A-B)=0.7-0.5=0.2$

</div>
<div style='float: right; width:30%;'>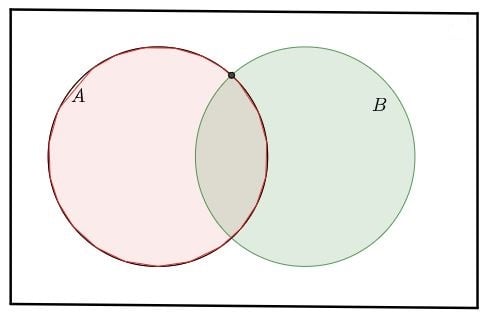

![alt text](https://imagedelivery.net/YfdZ0yYuJi8R0IouXWrMsA/a553b4ea-57b9-469d-40b1-6a654d4f6200/public)

</main>
<hr>
<footer style = "font-size: 18px"> $\rightarrow$ Probability lecture-4 $\rightarrow$ <span style = "color:blue"> Problem-1 </span> $\rightarrow$ Solution $\rightarrow$ Problem-2 </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-2 </primary>
<hr>
<main>

- Let $A$ and $B$ be any two events with $P(A \cup B)=0.7$ $P(A)=0.5, P(B)=0.3$. Find $P\left(A \mid B^c\right)$.

- Solution:

- $P\left(A \mid B^c\right)=\frac{P\left(A \cap B^c\right)}{P\left(B^c\right)}$

- From the addition rule

- $P(A \cup B)=  P(A)+P(B)-P(A \cap B)$

- $\Rightarrow P(A \cap B) =P(A)+P(B)-P(A \cup B)$

- =0.5+0.3-0.7=0.1

</div>
<div style='float: right; width:1%;'>

</div>

</main>
<hr>
<footer style = "font-size: 18px">Problem-1 $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Problem-2 </span> $\rightarrow$ Solution $\rightarrow$ Problem-3 </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-5 </primary>
<hr>
<main>

- A pair of fair dice is rolled until a sum of 7 appears. Find the probability that the sum 7 appears first on the $3^{\text {rd }}$ roll.

- solution : E = Sum is seven $\rightarrow\{(1,6),(6,1),(2,5),(5,2),(3,4),(4,3)}$

- $P(E)=\frac{6}{36}=\frac{1}{6}=p$

</div>
<div style='float: right; width:1%;'>

</div>
</main>
<hr>
<footer style = "font-size: 18px">Problem-4 $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Problem-5 </span> $\rightarrow$ Solution $\rightarrow$ Problem-6 </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-6 </primary>
<hr>
<main>

- Let $A$ and $B$ be two events which are independent with

- $P(A-B)=\frac{3}{25}, P(8-A)=\frac{8}{25}$. Further $P(A)>\frac{1}{2}$. Find $P(B)$.

- Solution : $\quad P(A-B)=P\left(A \cap B^c\right)=\frac{3}{25}$

- $P(B-A)=P\left(B \cap A^C\right)=\frac{8}{25}$

</div>
<div style='float: right; width:30%;'>

![alt text](https://imagedelivery.net/YfdZ0yYuJi8R0IouXWrMsA/a553b4ea-57b9-469d-40b1-6a654d4f6200/public)

</div>

</main>
<hr>
<footer style = "font-size: 18px">Problem-5 $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Problem-6 </span> $\rightarrow$ Solution $\rightarrow$ Solution </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Solution </primary>
<hr>
<main>

- $\Rightarrow \quad P(1-q)=\frac{3}{25} \cdots(1) \quad q=P(B)$

- $ P(B) P\left(A^c\right)=(1-p) q=\frac{8}{25} \cdots(2)$

- (2) - (1) gives $q-p=\frac{1}{5} \ldots$ (3)

- Using of from (3) in (2), we get,$(1-p)\left(p+\frac{1}{5}\right)=\frac{8}{25}$

- $-p^2+p-\frac{p}{5}+\frac{1}{5}=\frac{8}{25}$

- $-p^2+\frac{4 p}{5}-\frac{3}{25}=0 \Rightarrow-\left(\frac{1}{5}-p\right)\left(\frac{3}{5}-p\right)=0$

- $\Rightarrow p=\frac{1}{5} \text { or } \frac{3}{5} \text {. Since } p>\frac{1}{2} \text {, we take }$  ,$P(A)=\frac{3}{5} \Rightarrow P(B)=\frac{4}{5}$

</div>

</main>
<hr>
<footer style = "font-size: 18px">Problem-6 $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Solution </span> $\rightarrow$ Problem-7 $\rightarrow$ Solution </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-7 </primary>
<hr>
<main>

-  Two fair dice are tossed together. What is the probability that the product of the numbers is divisible by 6 ?

- Solution: The total number of outcomes $=36$
</div>
<div style='float: right; width:1%;'>

</main>
<hr>
<footer style = "font-size: 18px">Solution $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Problem-7 </span> $\rightarrow$ Solution $\rightarrow$ Problem-8 </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-8 </primary>
<hr>
<main>

-  In this problem what is the conditional probability that the sum of the numbers is at least 10 given that the product is divisible by 6 ?

- Solution:  $B \rightarrow$ sum is at least 10 .

- $P(A)=\frac{15}{36}=\frac{5}{12}$

- $ B=\{(4,6),(5,5),(5,6),(6,4),(6,5),(6,6)\}$

- $ P(B \mid A)=\frac{P(A \cap B)}{P(A)}=\frac{5 / 36}{5 / 12}=\frac{1}{3}$  .

</div>
<div style='float: right; width:1%;'>

</main>
<hr>
<footer style = "font-size: 18px">Problem-7 $\rightarrow$ Solution $\rightarrow$ <span style = "color:blue"> Problem-8 </span> $\rightarrow$ Problem-9 $\rightarrow$ Problem-10 </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-9 </primary>
<hr>
<main>

- An experiment has two possible outcomes, the first occurs with prob. $p^2+p / 4$ and the second with prob. $\frac{3-p}{4}$. What is the value of $p$ ?

- solution.

- $ p^2+\frac{p}{4}+\frac{3-p}{4}=1 \Rightarrow p^2=\frac{1}{4}$

- $\Rightarrow  p= \pm \frac{1}{2}$

- $p=\frac{1}{2} \longrightarrow$ the probabilities of two outcomes are $\frac{3}{8}$ and $\frac{5}{8}$

- $p=-\frac{1}{2} \longrightarrow$ the pribatilites of two outcomes are. $\frac{1}{8}$ and $\frac{7}{8}$  
</div>
<div style='float: right; width:1%;'>

</main>
<hr>
<footer style = "font-size: 18px">Solution $\rightarrow$ Problem-8 $\rightarrow$ <span style = "color:blue"> Problem-9 </span> $\rightarrow$ Problem-10 $\rightarrow$ Thank you </footer>

### <Success style="font-size:25px"> Probability Some Problems On Probability L-4 </Success>
### <primary style="font-size:24px"> Problem-10 </primary>
<hr>
<main>

-  Each of coefficients $a, b, c$ in the system of linear equations $\quad a x+b y=0$

- and  b x+c y=0

- is determined by tossing a fair die. What is the probability that the system has nontrivial solutions?

- Soln.  The condition is $a c-b^2=0$

- {(1,1,1),(1,2,4),(4,2,1),(2,2,2)
- (3,3,3),(4,4,4),(5,5,5),(6,6,6)}

- $\rightarrow \text { cos } \rightarrow 8$

- $\text { Reqd Prb }=\frac{8}{6^3}=\frac{8}{216}=\frac{1}{27}$

</div>
<div style='float: right; width:1%;'>

</main>
<hr>
<footer style = "font-size: 18px">Problem-8 $\rightarrow$ Problem-9 $\rightarrow$ <span style = "color:blue"> Problem-10 </span> $\rightarrow$ Thank you $\rightarrow$  </footer>