Lcr Circuits- Analytical Solution Resonance

LCR Circuits- Analytical Solution Resonance - Resonance

In LCR circuits, an inductor (L), a capacitor (C), and a resistor (R) are connected in series or parallel.
The behavior of LCR circuits can be analyzed using differential equations or through phasor diagrams.
Analytical solutions involve finding the current and voltage expressions as functions of time.
Resonance occurs when the frequency of the driving source matches the natural frequency of the LCR circuit.
At resonance,
- Impedance is at its minimum value.
- Current is at its maximum value.
- Energy transfer between the inductor and capacitor is maximized.

LCR Circuits- Analytical Solution Resonance - Differential Equations

The differential equation for an LCR circuit is derived from Kirchhoff’s laws.
The general differential equation for an LCR circuit connected in series is: $L\frac{d^2i}{dt^2}+ R\frac{di}{dt}+ \frac{i}{C} = V_0\sin(\omega t + \phi)$
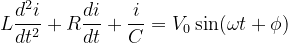
The solution to the differential equation gives the time-varying current (i(t)) and voltage (v(t)).
Parameters in the differential equation:
- L: Inductance (measured in henries, H)
- R: Resistance (measured in ohms, Ω)
- C: Capacitance (measured in farads, F)
- V₀: Peak voltage of the driving source
- ω: Angular frequency (measured in radians/second)
- φ: Phase angle

LCR Circuits- Analytical Solution Resonance - Phasor Diagram

Phasor diagrams provide a graphical representation of the voltages and currents in LCR circuits.
Phasors are vectors that represent the magnitudes and phase differences of AC quantities.
In an LCR circuit at resonance:
- The current phasor is in phase with the driving voltage phasor.
- The voltage across the inductor and capacitor cancel out, resulting in a minimum voltage across the resistor.
- The inductive and capacitive reactances are equal, leading to a minimum total impedance.

LCR Circuits- Analytical Solution Resonance - Impedance

The impedance (Z) of an LCR circuit is the total opposition to the flow of current.
It is the complex sum of the resistance (R), inductive reactance (XL), and capacitive reactance (XC): $Z = R + j(X_L - X_C)$ where j is the imaginary unit.
At resonance, the impedance is given by: $Z = R$

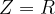
LCR Circuits- Analytical Solution Resonance - Current and Voltage

The current through the LCR circuit at resonance can be calculated using Ohm’s law: $I = \frac{V_0}{R}$
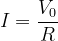
The voltage across the resistor at resonance is given by: $V_R = V_0$
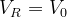
The voltage across the inductor and capacitor cancel out, resulting in zero voltage across each component.

LCR Circuits- Analytical Solution Resonance - Power

The power in an LCR circuit can be calculated using the instantaneous power equation: $P = VI\cos(\theta)$ where V is the instantaneous voltage, I is the instantaneous current, and θ is the phase angle.
At resonance, the power factor is unity (cos(θ) = 1), meaning power is fully transferred to the resistor.
The power dissipated in the resistor is given by: $P = \frac{V_0^2}{R}$

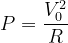
LCR Circuits- Analytical Solution Resonance - Example 1

Consider an LCR circuit with the following values:
- Inductance (L): 2 H
- Capacitance (C): 0.1 μF
- Resistance (R): 100 Ω
- Driving voltage (V₀): 10 V (peak)
Calculate the current through the circuit and the power dissipated in the resistor at resonance.

LCR Circuits- Analytical Solution Resonance - Example 2

Consider another LCR circuit with the following values:
- Inductance (L): 4 mH
- Capacitance (C): 100 nF
- Resistance (R): 1 kΩ
- Driving voltage (V₀): 5 V (peak)
Calculate the current through the circuit and the voltage across the resistor at resonance.

LCR Circuits- Analytical Solution Resonance - Summary

LCR circuits involve the interplay of inductance, capacitance, and resistance.
Analytical solutions involve solving differential equations or using phasor diagrams.
Resonance occurs when the driving frequency equals the natural frequency of the LCR circuit.
At resonance, impedance is minimized, current is maximized, and power is fully transferred to the resistor.
Calculations can be performed to determine current, voltage, power, and other circuit parameters.

LCR Circuits- Analytical Solution Resonance - Differential Equations

The differential equation for an LCR circuit is derived from Kirchhoff’s laws.
The general differential equation for an LCR circuit connected in series is: $L\frac{d^2i}{dt^2}+ R\frac{di}{dt}+ \frac{i}{C} = V_0\sin(\omega t + \phi)$
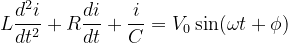
The solution to the differential equation gives the time-varying current (i(t)) and voltage (v(t)).
Parameters in the differential equation:
- L: Inductance (measured in henries, H)
- R: Resistance (measured in ohms, Ω)
- C: Capacitance (measured in farads, F)
- V₀: Peak voltage of the driving source
- ω: Angular frequency (measured in radians/second)
- φ: Phase angle

LCR Circuits- Analytical Solution Resonance - Phasor Diagram

Phasor diagrams provide a graphical representation of the voltages and currents in LCR circuits.
Phasors are vectors that represent the magnitudes and phase differences of AC quantities.
In an LCR circuit at resonance:
- The current phasor is in phase with the driving voltage phasor.
- The voltage across the inductor and capacitor cancel out, resulting in a minimum voltage across the resistor.
- The inductive and capacitive reactances are equal, leading to a minimum total impedance.

LCR Circuits- Analytical Solution Resonance - Impedance

The impedance (Z) of an LCR circuit is the total opposition to the flow of current.
It is the complex sum of the resistance (R), inductive reactance (XL), and capacitive reactance (XC): $Z = R + j(X_L - X_C)$ where j is the imaginary unit.
At resonance, the impedance is given by: $Z = R$

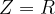
LCR Circuits- Analytical Solution Resonance - Current and Voltage

The current through the LCR circuit at resonance can be calculated using Ohm’s law: $I = \frac{V_0}{R}$
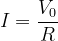
The voltage across the resistor at resonance is given by: $V_R = V_0$
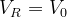
The voltage across the inductor and capacitor cancel out, resulting in zero voltage across each component.

LCR Circuits- Analytical Solution Resonance - Power

The power in an LCR circuit can be calculated using the instantaneous power equation: $P = VI\cos(\theta)$ where V is the instantaneous voltage, I is the instantaneous current, and θ is the phase angle.
At resonance, the power factor is unity (cos(θ) = 1), meaning power is fully transferred to the resistor.
The power dissipated in the resistor is given by: $P = \frac{V_0^2}{R}$

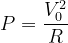
LCR Circuits- Analytical Solution Resonance - Resonance

Resonance is an important phenomenon in LCR circuits.
It occurs when the driving frequency matches the natural frequency of the circuit.
At resonance, the current through the circuit is at its maximum value.
Resonance can be observed by measuring the voltage across the components at different frequencies.
The resonance frequency can be calculated using the formula: $f_r = \frac{1}{2\pi\sqrt{LC}}$

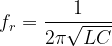
LCR Circuits- Analytical Solution Resonance - Example

Consider an LCR circuit with the following values:
- Inductance (L): 10 mH
- Capacitance (C): 100 μF
- Resistance (R): 1 kΩ
Calculate the resonance frequency for this circuit.
- Using the formula: $f_r = \frac{1}{2\pi\sqrt{LC}}$
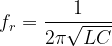
- Substituting the given values: $f_r = \frac{1}{2\pi\sqrt{(10 \times 10^{-3})(100 \times 10^{-6})}}$
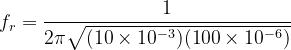
- Calculating the value: $f_r = 25.13 Hz$
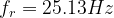
Therefore, the resonance frequency for this circuit is 25.13 Hz.

LCR Circuits- Analytical Solution Resonance - Quality Factor

The quality factor (Q) describes the sharpness of resonance in an LCR circuit.
It is a dimensionless quantity defined as the ratio of reactance to resistance: $Q = \frac{X}{R}$
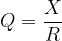
A higher quality factor indicates a narrower resonance bandwidth and a more selective circuit.
The quality factor can also be calculated using the formula: $Q = \frac{L}{R}C$
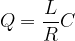
The quality factor determines the rate of energy loss in the circuit.

LCR Circuits- Analytical Solution Resonance - Example

Consider an LCR circuit with the following values:
- Inductance (L): 5 mH
- Capacitance (C): 10 μF
- Resistance (R): 100 Ω
Calculate the quality factor for this circuit.
- Using the formula: $Q = \frac{L}{R}C$
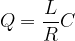
- Substituting the given values: $Q = \frac{5 \times 10^{-3}}{100 \times 10^{3}\times 10^{-6}}$
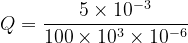
- Calculating the value: $Q = 0.5$
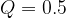
Therefore, the quality factor for this circuit is 0.5.

LCR Circuits- Analytical Solution Resonance - Bandwidth

The bandwidth (Δf) of an LCR circuit describes the range of frequencies around resonance.
It is defined as the difference between the upper and lower half-power frequencies. $\Delta f = f_2 - f_1$
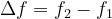
The half-power frequencies can be calculated using the formula: $f_2 - f_1 = \frac{f_r}{Q}$
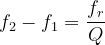
The bandwidth determines the range of frequencies over which the circuit responds efficiently.

LCR Circuits- Analytical Solution Resonance - Example

Consider an LCR circuit with the following values:
- Resonance frequency (fr): 1 kHz
- Quality factor (Q): 10
Calculate the bandwidth for this circuit.
- Using the formula: $\Delta f = \frac{f_r}{Q}$
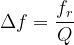
- Substituting the given values: $\Delta f = \frac{1000}{10}$
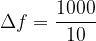
- Calculating the value: $\Delta f = 100 Hz$
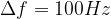
Therefore, the bandwidth for this circuit is 100 Hz.

LCR Circuits- Analytical Solution Resonance - Applications

LCR circuits find a wide range of applications in various fields.
They are used for filtering and selecting specific frequencies in electronic circuits.
LCR circuits form the basis of many communication systems, including radios and televisions.
They are also used in electronic amplifiers and audio systems.
LCR circuits are vital in designing power supplies and other equipment requiring precise control of current and voltage.