Integral Calculus - Solved Problems (Multiple Choice)

Integral Calculus - Solved Problems (Multiple Choice)

Integral Calculus - Solved Problems (Multiple Choice)

Slide 11:

Question: Find the indefinite integral of the function: $\frac{1}{x}$
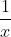
Options:
1. $\ln |x| + C$
2. $\frac{1}{2} \ln |x| + C$
3. $\ln |x|$
4. $\ln |x| - C$
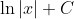
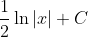
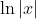
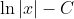
5. None of the above

Slide 12:

Solution: $\int \frac{1}{x} dx$
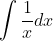
Applying the power rule, we get: $\ln |x| + C$
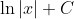
Therefore, the correct option is option 1. $\ln |x| + C$

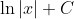
Slide 13:

Question: Evaluate the definite integral of the function: $\int_{1}^{3} x^{2} dx$
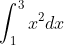
Options:
1. 6
2. 7
3. 9
4. 10
5. None of the above

Slide 14:

Solution: $\int_{1}^{3} x^{2} dx$
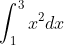
Applying the power rule, we get: $\left[\frac{1}{3} x^{3}\right]_{1}^{3} = \left[\frac{1}{3} (3)^{3} - (1)^{3}\right]$
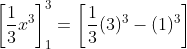
Simplifying, we get: $\frac{1}{3} (18 - 1) = \frac{17}{3}$
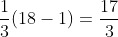
Therefore, the correct option is option 5. None of the above.

Slide 15:

Question: Find the definite integral of the function: $\int_{-1}^{1} \sqrt{1 - x^{2}} dx$
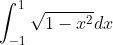
Options:
1. 1.57
2. 0.86
3. -2.34
4. 2.34
5. None of the above

Slide 16:

Solution: $\int_{-1}^{1} \sqrt{1 - x^{2}} dx$
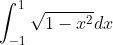
This represents the area under the semicircle with radius 1.
The area under a semicircle is half the area of the circle, which is $\frac{\pi}{2}$ .
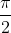Therefore, the correct option is option 5. None of the above.

Slide 17:

Question: Find the indefinite integral of the function: $\frac{\sin x}{\cos x}$
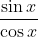
Options:
1. $\ln |\sin x + \cos x| + C$
2. $\ln |\tan x| + C$
3. $\ln |\csc x \cot x| + C$
4. $\ln (\sin x + \cos x) + C$
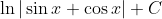
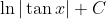
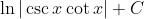
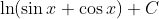
5. None of the above

Slide 18:

Solution: $\int \frac{\sin x}{\cos x} dx$
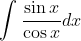
We can rewrite the function as: $\int \tan x dx$
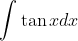
Applying the identity tan(x) = sin(x)/cos(x), we get: $\ln |\tan x| + C$
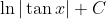
Therefore, the correct option is option 2. $\ln |\tan x| + C$

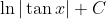
Slide 19:

Question: Find the definite integral of the function: $\int_{0}^{\pi} \sin^{2} x dx$
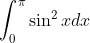
Options:
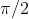
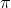
1. $\pi / 2$
2. 1
3. $\pi$
4. 2
5. None of the above

Slide 20:

Solution: $\int_{0}^{\pi} \sin^{2} x dx$
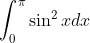
Applying the double angle identity sin^2(x) = (1 - cos(2x))/2, we get: $\int_{0}^{\pi} \frac{1}{2} (1 - \cos(2x))) dx$
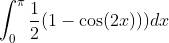
Expanding and integrating, we get: $\left[\frac{x}{2} - \frac{\sin(2x)}{4} \right]_{0}^{\pi} = \left[\frac{\pi}{2} - 0 \right] = \frac{\pi}{2}$
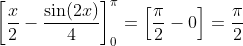
Therefore, the correct option is option 1. $\pi / 2$

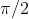
Integral Calculus - Solved Problems (Multiple Choice)

Slide 21:

Question: Find the indefinite integral of the function: $\int \frac{1}{\sqrt{x}} dx$
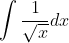
Options:
1. $2 \sqrt{x} + C$
2. $\frac{2}{3} x\sqrt{x} + C$
3. $2 x\sqrt{x} + C$
4. $\frac{2}{3} \sqrt{x} + C$
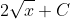
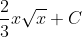
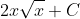
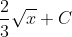
5. None of the above

Slide 22:

Solution: $\int \frac{1}{\sqrt{x}} dx$
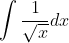
Applying the power rule, we get: $2 \sqrt{x} + C$
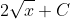
Therefore, the correct option is option 1. $2 \sqrt{x} + C$

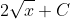
Slide 23:

Question: Evaluate the definite integral of the function: $\int_{0}^{\frac{\pi}{2}} \cos^{2} x dx$
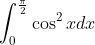
Options:
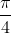
1. $\frac{\pi}{4}$
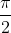
2. 1
3. $\frac{\pi}{2}$
4. 2
5. None of the above

Slide 24:

Solution: $\int_{0}^{\frac{\pi}{2}} \cos^{2} x dx$
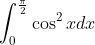
From the double angle identity cos^2(x) = (1 + cos(2x))/2, we get: $\int_{0}^{\frac{\pi}{2}} \frac{1}{2} (1 + \cos(2x))) dx$
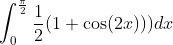
Expanding and integrating, we get: $\left[\frac{x}{2} + \frac{\sin(2x)}{4} \right]_{0}^{\frac{\pi}{2}} = \left[\frac{\pi}{4} + 0 \right] = \frac{\pi}{4}$
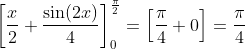
Therefore, the correct option is option 1. $\frac{\pi}{4}$

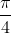
Slide 25:

Question: Find the indefinite integral of the function: $\int e^{\sqrt{x}} dx$
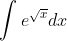
Options:
1. $2e^{\sqrt{x}} + C$
2. $\frac{2}{3} x e^{\sqrt{x}} + C$
3. $2 x e^{\sqrt{x}} + C$
4. $\frac{2}{3} e^{\sqrt{x}} + C$
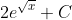
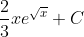
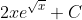
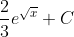
5. None of the above

Slide 26:

Solution: $\int e^{\sqrt{x}} dx$
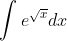
Making the substitution u = 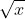$\sqrt{x}$ , we get: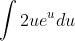 $\int 2u e^{u} du$
This is a standard integral. Solving it, we get: $2e^{\sqrt{x}} + C$
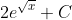
Therefore, the correct option is option 1. $2e^{\sqrt{x}} + C$

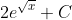
Slide 27:

Question: Find the definite integral of the function: $\int_{0}^{1} (x - 1)^{6} dx$
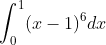
Options:
1. -0.035
2. 0.035
3. -0.023
4. 0.023
5. None of the above

Slide 28:

Solution: ![equation](https://latex.codecogs.com/gif.lat