Continuity and Differentiability - An introduction
- Definition of continuity: A function is said to be continuous at a point if the limit of the function at that point exists
- Types of discontinuities: Removable, jump, and infinite discontinuity
- Definition of differentiability: A function is said to be differentiable at a point if the derivative of the function exists at that point
- Differentiable implies continuous, but continuous does not imply differentiable
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions2
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions3
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions4
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions5
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions6
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions7
The Derivative
- The derivative of a function measures how the function changes as its input changes
- Definition of the derivative: The derivative of a function f(x) at a point x = a is defined by the limit:
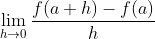
- Notation for derivative:
 ,
,  , or
, or 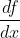
Differentiation Rules
- Constant rule: The derivative of a constant c is 0:
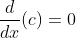
- Power rule: If
 exists, then
exists, then  for all real numbers n
for all real numbers n
- Sum/Difference rule: If
 exist, then
exist, then 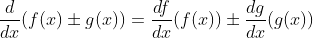
Chain Rule
- The chain rule allows us to differentiate composite functions
- Statement of the chain rule: If g(x) is differentiable at x=a and f(x) is differentiable at g(a), then the composite function (f ∘ g)(x) is differentiable at x=a and its derivative is given by:
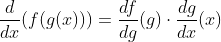
Examples
- Example 1: Differentiate
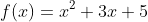
- Example 2: Differentiate
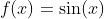
- Example 3: Find the derivative of the function
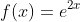
- Example 4: Use the chain rule to differentiate
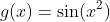
Higher Derivatives
- The second derivative of a function is the derivative of its first derivative
- Notation for second derivative:
 ,
,  , or
, or 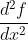
- Higher derivatives can also be defined by taking successive derivatives
Trigonometric Functions
- Definitions of trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent
- Trig identities: Pythagorean identities, double angle identities, and reciprocal identities
- Derivatives of trigonometric functions:
Limits and Continuity
- Definition of a limit: A function f(x) approaches a limit L as x approaches a point c, denoted by
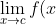%20%3D%20L)
- Basic properties of limits: Sum/difference, product, quotient, and power rules
- Definition of continuity: A function f(x) is continuous at a point c if:
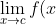) exists
exists) is defined
is defined
- Types of discontinuities: Removable, jump, and infinite discontinuity
- Continuity and Differentiability - An introduction
- Definition of continuity: A function is said to be continuous at a point if the limit of the function at that point exists.
- Types of discontinuities: Removable, jump, and infinite discontinuity.
- Definition of differentiability: A function is said to be differentiable at a point if the derivative of the function exists at that point.
- Differentiable implies continuous, but continuous does not imply differentiable.
- Common examples of continuous and differentiable functions: Polynomial functions, exponential functions, and trigonometric functions.
- The Derivative
- The derivative of a function measures how the function changes as its input changes.
- Definition of the derivative: The derivative of a function f(x) at a point x = a is defined by the limit:
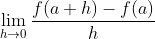 .
.
- Notation for derivative:
 ,
,  , or
, or 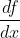 .
.
- Differentiation Rules
- Constant rule: The derivative of a constant c is 0:
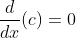 .
.
- Power rule: If
 exists, then
exists, then  for all real numbers n.
for all real numbers n.
- Sum/Difference rule: If
 exist, then
exist, then 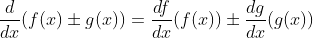 .
.
- Chain Rule
- The chain rule allows us to differentiate composite functions.
- Statement of the chain rule: If g(x) is differentiable at x=a and f(x) is differentiable at g(a), then the composite function (f ∘ g)(x) is differentiable at x=a and its derivative is given by:
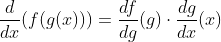 .
.
- Examples
- Example 1: Differentiate
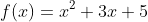 .
.
- Example 2: Differentiate
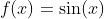 .
.
- Example 3: Find the derivative of the function
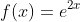 .
.
- Example 4: Use the chain rule to differentiate
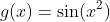 .
.
- Higher Derivatives
- The second derivative of a function is the derivative of its first derivative.
- Notation for second derivative:
 ,
,  , or
, or 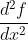 .
.
- Higher derivatives can also be defined by taking successive derivatives.
- Trigonometric Functions
- Definitions of trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent.
- Trig identities: Pythagorean identities, double angle identities, and reciprocal identities.
- Derivatives of trigonometric functions:
- Limits and Continuity
- Definition of a limit: A function f(x) approaches a limit L as x approaches a point c, denoted by
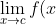%20%3D%20L) .
.
- Basic properties of limits: Sum/difference, product, quotient, and power rules.
- Definition of continuity: A function f(x) is continuous at a point c if:
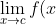) exists
exists) is defined.
is defined.
- Types of discontinuities
- Removable discontinuity: A point at which a function is undefined, but the limit as x approaches that point exists and can be made equal to the value obtained by defining the function at that point.
- Jump discontinuity: A point at which the function has a finite jump in value.
- Infinite discontinuity: A point at which the limit of the function as x approaches the point is either infinite or does not exist.
- Example: Removable Discontinuity
- The function
 has a removable discontinuity at x = 2.
has a removable discontinuity at x = 2.
- By simplifying the expression, we can rewrite the function as f(x) = x + 2.
- The limit of f(x) as x approaches 2 is equal to the value of the function f at x = 2, which
,
, or
exists, then
for all real numbers n
exist, then
,
, or
exists
is defined
.
,
, or
.
.
exists, then
for all real numbers n.
exist, then
.
.
.
.
.
.
,
, or
.
.
exists
is defined.
has a removable discontinuity at x = 2.