Work Energy and Power - Result Question 53
56. Two spheres $A$ and $B$ of masses $m_1$ and $m_2$ respectively collide. $A$ is at rest initially and $B$ is moving with velocity $v$ along $x$-axis. After collision $B$ has a velocity $\frac{v}{2}$ in a direction perpendicular to the original direction. The mass $A$ moves after collision in the direction.
(a) Same as that of $B$
[2012]
(b) Opposite to that of $B$
(c) $\theta=\tan ^{-1}(1 / 2)$ to the $x$-axis
(d) $\theta=\tan ^{-1}(-1 / 2)$ to the $x$-axis
Show Answer
Answer:
Correct Answer: 56. (d)
Solution:
- (d)
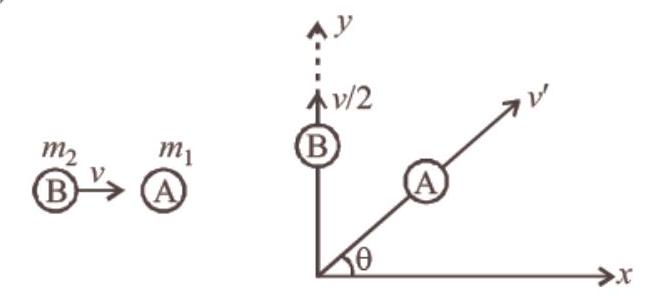
[Before collision]
[After collision] According to law of conservation of linear momentum along $x$-axis, we get
$\Rightarrow m_1(0)+m_2 v=m_1 v^{\prime} \cos \theta$
$\Rightarrow \cos \theta=\frac{m_2 v}{m_1 v^{\prime}}$
Similarly, law of conservation of linear momentum along $y$-axis, we get
$\Rightarrow m_1(0)+m_2(0)=m_1 v^{\prime} \sin \theta+m_2(\frac{v}{2})$
$\Rightarrow \sin \theta=\frac{m_2 v}{2 m_1 v^{\prime}}$
From equations, (i) and (ii),
$\tan \theta=-(\frac{m_2 v}{2 m v^{\prime}}) \times(\frac{m_1 v^{\prime}}{m_2 v})=-\frac{1}{2}$
$\theta=\tan ^{-1}(\frac{-1}{2})$ to the $x$-axis.
Let A moves in the direction, which makes an angle $\theta$ with initial direction i.e.,
$\tan \theta=\frac{v_y}{v_x}=\frac{m_2 v}{2 m_1} / \frac{m_2 v}{2 m_1}$
$\tan \theta=\frac{1}{2}$
$\Rightarrow \theta=\tan ^{-1}(\frac{1}{2})$ to the $x$-axis.










