Work Energy and Power - Result Question 48
51. On a frictionless surface a block of mass $M$ moving at speed $v$ collides elastically with another block of same mass $M$ which is initially at rest. After collision the first block moves at an angle $\theta$ to its initial direction and has a speed
$\frac{v}{3}$. The second block’s speed after the collision is :
[2015 RS]
(a) $\frac{3}{4} v$
(b) $\frac{3}{\sqrt{2}} v$
(c) $\frac{\sqrt{3}}{2} v$
(d) $\frac{2 \sqrt{2}}{3} v$
Show Answer
Answer:
Correct Answer: 51. (d)
Solution:
- (d) Here, $M_1=M_2$ and $u_2=0$
$ u_1=V, \quad V_1=\frac{V}{3} ; \quad V_2=? $
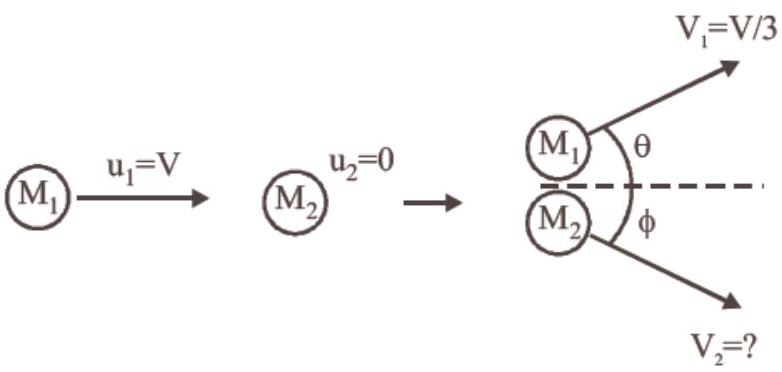
From figure, along $x$-axis,
$M_1 u_1+M_2 u_2=M_1 V_1 \cos \theta+M_2 V_2 \cos \phi \ldots$ (i) Along $y$-axis
$0=M_1 V_1 \sin \theta-M_2 V_s \sin \phi$
By law of conservation of kinetic energy,
$\frac{1}{2} M_1 u_1^{2}+\frac{1}{2} M_2 u_2^{2}=\frac{1}{2} M_1 V_1^{2}+\frac{1}{2} M_2 V_2^{2}$
Putting $M_1=M_2$ and $u_2=0$ in equation (i), (ii) and (iii) we get,
$\theta+\phi=\frac{\pi}{2}=90^{\circ}$
and $u_1^{2}=V_1^{2}+V_2^{2}$
$V^{2}=(\frac{V}{3})^{2}+V_2^{2}[\because u_1=V.$ and $.V_1=\frac{V}{3}]$
or, $V^{2}-(\frac{V}{3})^{2}=V_2^{2}$
$V^{2}-\frac{V^{2}}{9}=V_2^{2}$
or $V_2^{2}=\frac{8}{9} V^{2} \Rightarrow V_2=\frac{2 \sqrt{2}}{3} V$










