Work Energy and Power - Result Question 23
26. In a simple pendulum of length $l$ the bob is pulled aside from its equilibrium position through an angle $\theta$ and then released. The bob passes through the equilibrium position with speed
[2000]
(a) $\sqrt{2 g \ell(1+\cos \theta)}$
(b) $\sqrt{2 g \ell \sin \theta}$
(c) $\sqrt{2 g \ell}$
(d) $\sqrt{2 g \ell(1-\cos \theta)}$
Show Answer
Answer:
Correct Answer: 26. (d)
Solution:
- (d) If1 is length of pendulum and $\theta$ be angular amplitude then height
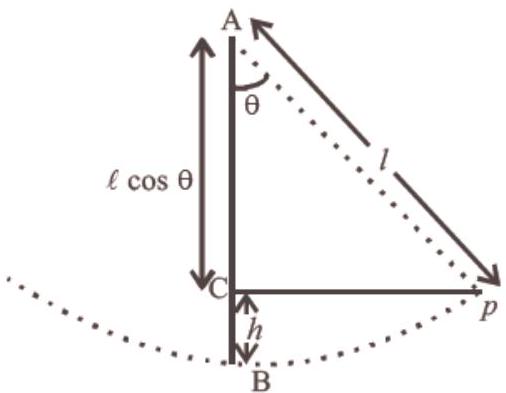
$h=AB-AC=1-1 \cos \theta=1(1-\cos \theta)$
At extreme position, potential energy is maximum and kinetic energy is zero; At mean (equilibrium) position potential energy is zero and kinetic energy is maximum, so from principle of conservation of energy.
$(KE+PE)$ at $P=(KE+PE)$ at $B$
$0+m g h=\frac{1}{2} m v^{2}+0$
$\Rightarrow v=\sqrt{2 g h}=\sqrt{2 g \ell(1-\cos \theta)}$










