Wave Optics - Result Question 28
«««< HEAD:content/english/neet-pyq-chapterwise/physics/wave-optics/wave-optics-result-question-28.md
30. For a parallel beam of monochromatic light of wavelength ’ $\lambda$ ‘, diffraction is produced by a single slit whose width ’ $a$ ’ is of the wavelength of the light. If ’ $D$ ’ is the distance of the screen from the slit, the width of the central maxima will be :[2015]
======= ####30. For a parallel beam of monochromatic light of wavelength ’ $\lambda$ ‘, diffraction is produced by a single slit whose width ’ $a$ ’ is of the wavelength of the light. If ’ $D$ ’ is the distance of the screen from the slit, the width of the central maxima will be :[2015]
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/wave-optics/wave-optics—result-question-28.md (a) $\frac{D \lambda}{a}$
(b) $\frac{Da}{\lambda}$
(c) $\frac{2 Da}{\lambda}$
(d) $\frac{2 D \lambda}{a}$
Show Answer
Solution:
- (d) Linear width of central maxima $Y$
$=D(2 \theta)=2 D \theta=\frac{2 D \lambda}{a} \quad \therefore \theta=\frac{\lambda}{a}$
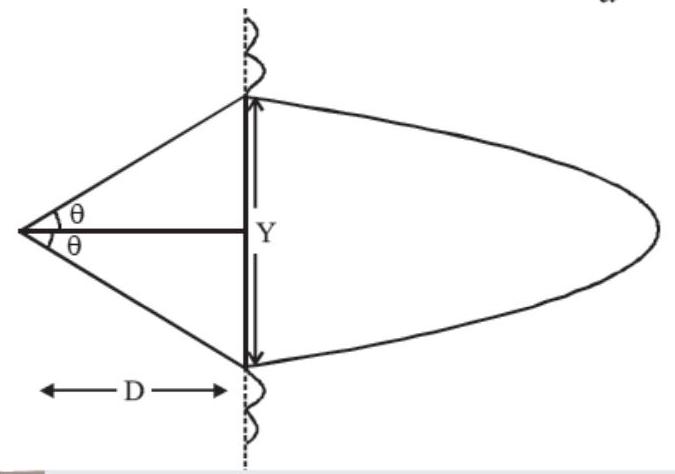
The central maxima lies between the first minima on both sides.
The angular width ’ $d$ ’ central maxima $=2 \theta=\frac{2 \lambda}{b}$
Linear width of central maxima $=2 D \theta=\frac{2 D \lambda}{b}$
$b=$ width of slits and $D=$ distance between slit and screen.










