System of Particles and Rotational Motion - Result Question 80
86. A solid cylinder of mass $m$ and radius $R$ rolls down an inclined plane of height $h$ without slipping. The speed of its centre of mass when it reaches the bottom is
[2003, 1989]
(a) $\sqrt{(2 g h)}$
(b) $\sqrt{4 g h / 3}$
(c) $\sqrt{3 g h / 4}$
(d) $\sqrt{4 g / h}$
Show Answer
Answer:
Correct Answer: 86. (b)
Solution:
$ \begin{aligned} \text{ (b) } & K . E .=\frac{1}{2} I \omega^{2}+\frac{1}{2} m v^{2} \\ K . E . & =\frac{1}{2}(\frac{1}{2} m r^{2}) \omega^{2}+\frac{1}{2} m v^{2} \\ & =\frac{1}{4} m v^{2}+\frac{1}{2} m v^{2}=\frac{3}{4} m v^{2} \end{aligned} $
Now, gain in K.E. $=$ Loss in P.E.
$ \begin{equation*} \frac{3}{4} m v^{2}=m g h \Rightarrow v=\sqrt{(\frac{4}{3}) g h} \tag{b} \end{equation*} $
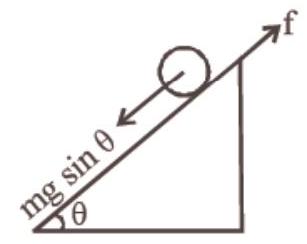
Torque, $I \alpha=f . R$.
Using Newton’s IInd law, $m g \sin \theta-f=m a$
$\because$ pure rolling is there, $a=R \alpha$
$\Rightarrow m g \sin \theta-\frac{I \alpha}{R}=m a$
$\Rightarrow m g \sin \theta-\frac{I a}{R^{2}}=m a \quad(\because \alpha=\frac{a}{R})$
or, acceleration, $a=\frac{m g \sin \theta}{(I / R^{2}+m)}$
Using, $s=u t+\frac{1}{2} a t^{2}$
or, $s=\frac{1}{2} a t^{2} \Rightarrow t \alpha \frac{1}{\sqrt{a}}$
$t$ minimum means a should be more. This is possible when $I$ is minimum which is the case for solid cylinder.
Therefore, solid cylinder will reach the bottom first.










