System of Particles and Rotational Motion - Result Question 78
«««< HEAD:content/english/neet-pyq-chapterwise/physics/system-of-particles-and-rotational-motion/system-of-particles-and-rotational-motion-result-question-78.md
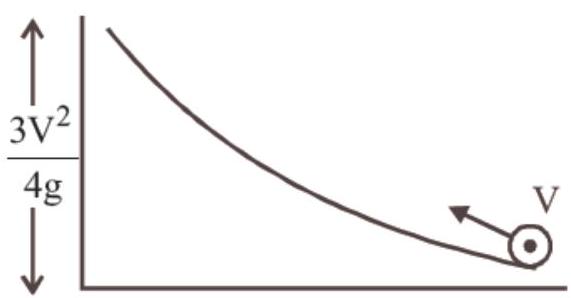
84. A small object of uniform density rolls up a curved surface with an initial velocity ’ $v$ ‘. It reaches upto a maximum height of $\frac{3 v^{2}}{4 g}$ with respect to the initial position. The object is a
======= ####84. A small object of uniform density rolls up a curved surface with an initial velocity ’ $v$ ‘. It reaches upto a maximum height of $\frac{3 v^{2}}{4 g}$ with respect to the initial position. The object is a
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/system-of-particles-and-rotational-motion/system-of-particles-and-rotational-motion—result-question-78.md (a) solid sphere
(b) hollow sphere
(c) disc
(d) ring
[2013]
Show Answer
Answer:
Correct Answer: 84. (c)
Solution:
- (c)
From law of conservation of mechanical energy,
$\Rightarrow \frac{1}{2} I \omega^{2}+0+\frac{1}{2} mv^{2}=mg \times \frac{3 v^{2}}{4 g}$
$\Rightarrow \frac{1}{2} I \omega^{2}=\frac{3}{4} mv^{2}-\frac{1}{2} mv^{2}$
$\Rightarrow \frac{1}{2} I \omega^{2}=\frac{mv^{2}}{2}(\frac{3}{2}-1)$
or, $\frac{1}{2} I(\frac{V^{2}}{R^{2}})=\frac{mv^{2}}{4}$ or, $I=\frac{1}{2} mR^{2}$
Hence, object is a disc.










