System of Particles and Rotational Motion - Result Question 62
65. The moment of inertia of a uniform circular disc of radius $R$ and mass $M$ about an axis touching the disc at its diameter and normal to the disc is
[2006, 2005]
(a) $\frac{2}{5} MR^{2}$
(b) $\frac{3}{2} MR^{2}$
(c) $\frac{1}{2} MR^{2}$
(d) $MR^{2}$
Show Answer
Answer:
Correct Answer: 65. (c)
Solution:
- (c) M.I. of a uniform circular disc of radius ’ $R$ ’ and mass ’ $M$ ’ about an axis passing though C.M. and normal to the disc is
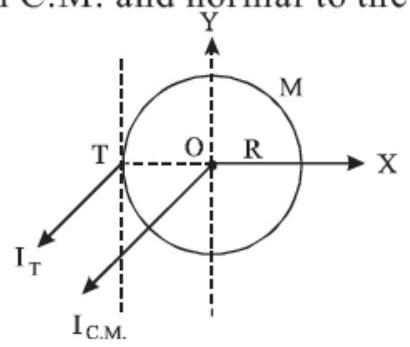
(d) As we know that,
Rotational energy $=\frac{1}{2} I(\omega)^{2}=\frac{1}{2}(m K^{2}) \omega^{2}$ And,
Linear kinetic energy $=\frac{1}{2} m \omega^{2} R^{2}$
$\therefore$ Required fraction,
$ =\frac{\frac{1}{2}(m K^{2}) \omega^{2}}{\frac{1}{2}(m K^{2}) \omega^{2}+\frac{1}{2} m \omega^{2} R^{2}}=(\frac{K^{2}}{K^{2}+R^{2}}) $
69 .
(b) Moment of inertia $=\int r^{2} d m$.
$\therefore$ Since, $\rho _{\text{iron }}>\rho _{\text{aluminium }}$
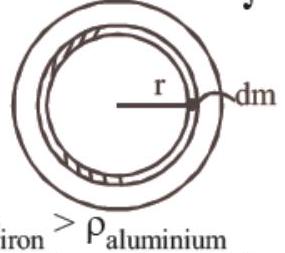
So, whole of aluminium is kept in the core and the iron at the outer rim of the disc.










