System of Particles and Rotational Motion - Result Question 54
58. Three identical spherical shells, each of mass $m$ and radius $r$ are placed as shown in figure. Consider an axis XX’ which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about XX’ axis is (a) $3 mr^{2}$
(b) $\frac{16}{5} mr^{2}$
(c) $4 mr^{2}$
(d) $\frac{11}{5} mr^{2}$

[2015]
Show Answer
Answer:
Correct Answer: 58. (c)
Solution:
- (c) Moment of inertia of shell 1 along diameter
$I _{\text{diameter }}=\frac{2}{3} Mr^{2}$
Moment of inertia of shell $2=$ M.I of shell 3
$=I _{\text{tangential }}=\frac{2}{3} Mr^{2}+Mr^{2}=\frac{5}{3} Mr^{2}$
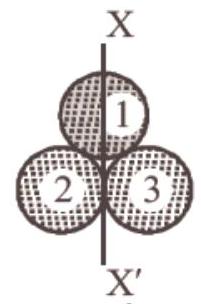
So, I of the system along $XX^{\prime}$
$=I _{\text{diameter }}+(I _{\text{tangential }}) \times 2$
or, $I _{\text{total }}=\frac{2}{3} Mr^{2}+(\frac{5}{3} Mr^{2}) \times 2$
$=\frac{12}{3} Mr^{2}=4 Mr^{2}$










