System of Particles and Rotational Motion - Result Question 38
40. A tube of length $L$ is filled completely with an incompressible liquid of mass $M$ and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity $\omega$. The force exerted by the liquid at the other end is
[2006]
(a) $\frac{M L^{2} \omega}{2}$
(b) $M L \omega^{2}$
(c) $\frac{M L^{2} \omega^{2}}{2}$
(d) $\frac{M L \omega^{2}}{2}$
Show Answer
Answer:
Correct Answer: 40. (d)
Solution:
- (d) therefore, $L_A=L_B$.
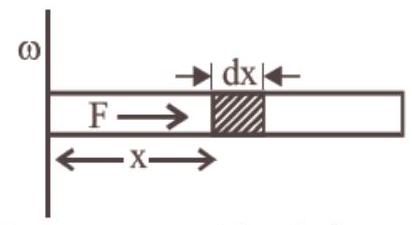
Rotation will create centrifugal force due to which pressure will be created at the other end. Now, this centrifugal force will depend on distance of the liquid from the axis as centrifugal force $=m \omega^{2} r$.
Let us consider a small part $dx$ of the liquid column which is at a distance of $x$.
Mass of this element will be, $dm=\frac{M}{L} dx$
So, force exerted on this element will be, $\Rightarrow df=dm . \omega^{2} x$
As the mass of liquid extends from $x=0$ to $x=L$, the net force on the wall experienced by the mass of the liquid is,
$ \begin{aligned} & \Rightarrow \int_0^{f} d f=\frac{M}{L} \int_0^{L} \omega^{2} \cdot x \cdot d x \\ & \Rightarrow \int_0^{f} d f=\frac{M}{L} \omega^{2} \int_0^{L} x \cdot d x \\ & \Rightarrow f=\frac{M}{L} \omega^{2}[\frac{L^{2}}{2}]=\frac{M \omega^{2} L}{2} \end{aligned} $










