System of Particles and Rotational Motion - Result Question 36
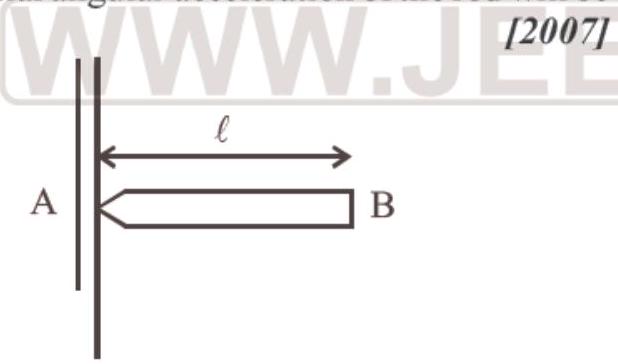
38. A uniform $rod A B$ of length $\ell$, and mass $m$ is free to rotate about point $A$. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is $\frac{m \ell^{2}}{3}$, the initial angular acceleration of the rod will be
(a) $\frac{m g \ell}{2}$
(b) $\frac{3}{2} g \ell$
(c) $\frac{3 g}{2 \ell}$
(d) $\frac{2 g}{3 \ell}$
Show Answer
Answer:
Correct Answer: 38. (c)
Solution:
(c)
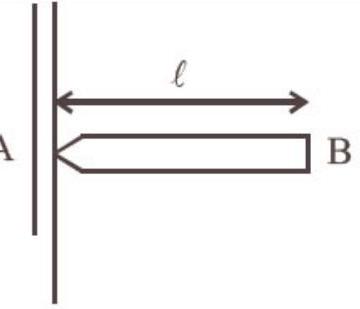
Weight of the rod will produce torque,
$\tau=m g \times \frac{\ell}{2}$
Also, $\tau=I \alpha$
where, $I$ is the moment of inertia $=\frac{m \ell^{2}}{3}$ and $\alpha$ is the angular acceleration
$\therefore \frac{m \ell^{2}}{3} \alpha=m g \times \frac{\ell}{2} \Rightarrow \alpha=\frac{3 g}{2 \ell}$










