Ray Optics and Optical Instruments - Result Question 30
30. A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive indices $\mu_1$ and $\mu_2$ and $R$ is the radius of curvature of the curved surface of the lenses, then the focal length of the combination is
[2013]
(a) $\frac{R}{2(\mu_1-\mu_2)}$
(b) $\frac{R}{(\mu_1-\mu_2)}$
(c) $\frac{2 R}{(\mu_2-\mu_1)}$
(d) $\frac{R}{2(\mu_1+\mu_2)}$
Show Answer
Answer:
Correct Answer: 30. (b)
Solution:
- (b) From the question,
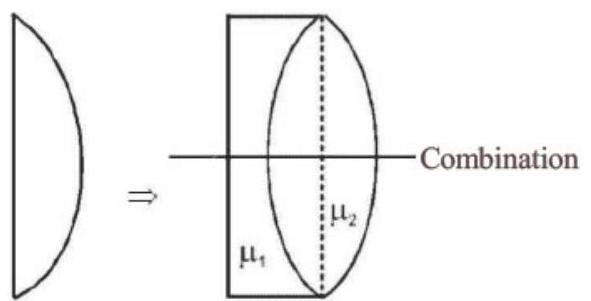
Plano-convex Plano-concave
$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$
$=(\mu_1-1)(\frac{1}{\infty}-\frac{1}{-R})+(\mu_2-1)(\frac{1}{\infty}-\frac{1}{R})$
$=\frac{(\mu_1-1)}{R}-\frac{(\mu_2-1)}{R} \Rightarrow \frac{1}{f}=\frac{\mu_1-\mu_2}{R}$
$\Rightarrow f=\frac{R}{\mu_1-\mu_2}$ Hence, focal length of the combination is
$\frac{R}{\mu_1-\mu_2}$.










