Ray Optics and Optical Instruments - Result Question 29
29. Two identical thin plano-convex glass lenses (refractive index 1.5) each having radius of curvature of $20 cm$ are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
[2015]
(a) $-25 cm$
(b) $-50 cm$
(c) $50 cm$
(d) $-20 cm$
Show Answer
Answer:
Correct Answer: 29. (b)
Solution:
- (b) Using lens maker’s formula,
$ \frac{1}{f}=(\mu-1)(\frac{1}{R_1}-\frac{1}{R_2}) $
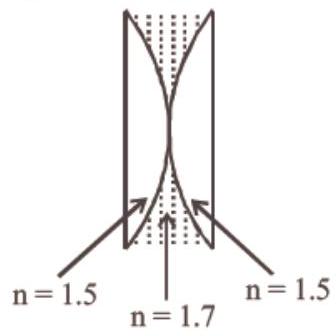 $\Rightarrow \frac{1}{f_1}=(\frac{1.5}{1}-1)(\frac{1}{\infty}-\frac{1}{-20})$
$\Rightarrow \frac{1}{f_1}=(\frac{1.5}{1}-1)(\frac{1}{\infty}-\frac{1}{-20})$
$\Rightarrow f_1=40 cm$
$\Rightarrow \frac{1}{f_2}=(\frac{1.7}{1}-1)(\frac{1}{-20}-\frac{1}{+20})$
$\Rightarrow f_2=-\frac{100}{7} cm$
Similarly,
$\Rightarrow \frac{1}{f_3}=(\frac{1.5}{1}-1)(\frac{1}{\infty}-\frac{1}{-20})$
$\Rightarrow f_3=40 cm$
Now according to the condition
$\frac{1}{f _{eq}}=\frac{1}{f_1}+\frac{1}{f_2}+\frac{1}{f_3}$
$\Rightarrow \frac{1}{f _{\text{eq }}}=\frac{1}{40}+\frac{1}{-100 / 7}+\frac{1}{40}$
$\therefore \quad f _{\text{eq }}=-50 cm$
Therefore, the focal length of the combination is $-50 cm$.
For a system of lenses net focal length $F _{\text{net }}$
$=\frac{1}{f_1}+\frac{1}{f_2}+\ldots+\frac{1}{f_n}$
Net power $P _{\text{net }}=P_1+P_2+\ldots+P_n$










