Oscillations - Result Question 48
52. A body of mass M, executes vertical SHM with periods $t_1$ and $t_2$, when separately attached to spring A and spring B respectively. The period of SHM, when the body executes SHM, as shown in the figure is $t_0$. Then
[2002]
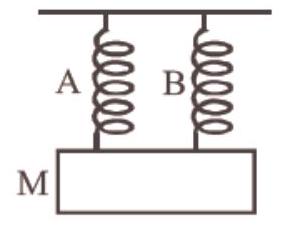
(a) $t_0^{-1}=t_1^{-1}+t_2^{-1}$
(b) $t_0=t_1+t_2$
(c) $t_0^{2}=t_1^{2}+t_2^{2}$
(d) $t_0{ }^{-2}=t_1{ }^{-2}+t_2{ }^{-2}$
Show Answer
Answer:
Correct Answer: 52. (d)
Solution:
- (d) The time period of spring mass system,
$ T=2 \pi \sqrt{\frac{m}{K}} $
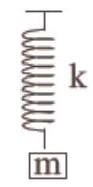
$\therefore \quad t_1=2 \pi \sqrt{\frac{m}{k_1}}$
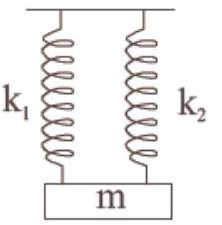
$ \begin{equation*} t_2=2 \pi \sqrt{\frac{m}{k_2}} \tag{ii} \end{equation*} $
When springs are connected in parallel then $K _{\text{eff }}=k_1+k_2$
So, $t_0=2 \pi \sqrt{\frac{m}{k _{eff}}} \Rightarrow 2 \pi \sqrt{\frac{m}{(k _{1+k_2})}}$
from (i), $\frac{1}{t_1^{2}}=\frac{1}{4 \pi^{2}} \times \frac{k_1}{m}$
from (ii), $\frac{1}{t_2^{2}}=\frac{1}{4 \pi^{2}} \times \frac{k_2}{m}$
from (iii), $\frac{1}{t_0^{2}}=\frac{1}{4 \pi^{2}} \times \frac{(k_1+k_2)}{m}$
from above expressions,
$\frac{1}{t_0^{2}}=\frac{1}{t_1^{2}}+\frac{1}{t_2^{2}}$
$ t=2 \pi \sqrt{\frac{m}{k}} $
$\Rightarrow \quad k=$ Const. $t^{-2}$
Here the springs are joined in parallel. So
$ k_0=k_1+k_2 $
where $k_0$ is resultant force constant
$\therefore$ Const. $t_0^{-2}=$ Const. $t_1^{-2}+$ Const. $t_2^{-2}$
or, $t_0^{-2}=t_1^{-2}+t_2^{-2}$










