Oscillations - Result Question 3
4. The displacement of a particle executing simple harmonic motion is given by
$y=A_0+A \sin \omega t+B \cos \omega t$.
[2019]
Then the amplitude of its oscillation is given by:
(a) $A_0+\sqrt{A^{2}+B^{2}}$
(b) $\sqrt{A^{2}+B^{2}}$
(c) $\sqrt{A_0^{2}+(A+B)^{2}}$
(d) $A+B$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- (b) $B$
Given equation
$y=A_0+A \sin \omega t+B \sin \omega t$
Now assume $(y-A_0)=\gamma$
$y-A_0=A \sin \omega t+B \sin \omega t$
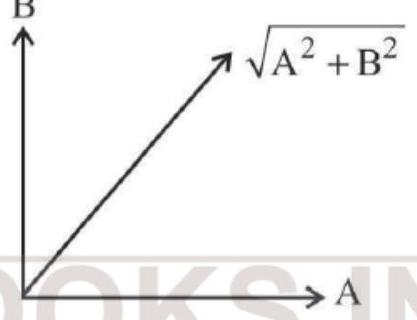
$\gamma=A \sin \omega t+B \cos \omega t$
$=\sqrt{A^{2}+B^{2}} \sin (\omega t+\phi)$
which is S.H.M.
where $\cos$
and $\sin \phi=\frac{B}{\sqrt{A^{2}+B^{2}}}$
so, resultant amplitude
$=\sqrt{A^{2}+B^{2}}$










