Oscillations - Result Question 1
1. The phase difference between displacement and acceleration of a particle in a simple harmonic motion is :
[2020]
(a) $\frac{3 \pi}{2} rad$
(b) $\frac{\pi}{2} rad$
(c) zero
(d) $\pi rad$
Show Answer
Solution:
- (d) Displacement equation of a SHM
$ y=A \sin (\omega t+\phi) $
$\therefore$ Velocity, $v=\frac{d y}{d t}=A \omega \cos (\omega t+\phi)$
Acceleration, $a=\frac{d v}{d t}$
$ \text{ or, } a=-A \omega^{2} \sin (\omega t+\phi) $
$ \therefore a=A \omega^{2} \sin (\omega t+\phi+\pi) $
Hence, phase difference between displacement and acceleration is $\pi$.
2 .
(d) Att $=0, y=3$, which is maximum displacement so equation will be cosine function.
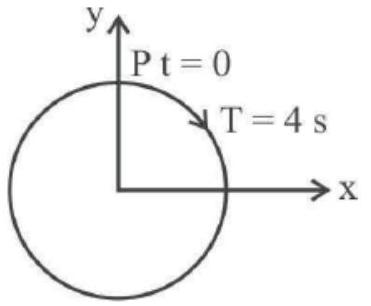
$ \begin{aligned} & \omega=\frac{2 \pi}{T}=\frac{2 \pi}{4}=\frac{\pi}{2} rad / s \quad(\because T=4 s) \\ & y=a \cos \omega t \Rightarrow y=3 \cos \frac{\pi}{2} t \end{aligned} $










