Moving Charges and Magnetism - Result Question 64
65. A current carrying loop in the form of a right angle isosceles triangle $A B C$ is placed in a uniform magnetic field acting along $AB$. If the magnetic force on the arm $BC$ is $F$, what is the force on the arm $AC$ ?
(a) $-\sqrt{2} \vec{F}$
(b) $-\overrightarrow{{}F}$
(c) $\overrightarrow{{}F}$
(d) $\sqrt{2} \overrightarrow{{}F}$
Show Answer
Answer:
Correct Answer: 65. (b)
Solution:
- (b) Let a current $i$ be flowing in the loop $A B C$ in the direction shown in the figure. If the length of each of the sides $AB$ and $BC$ be $x$ then $|\overrightarrow{{}F}|=i \times B$
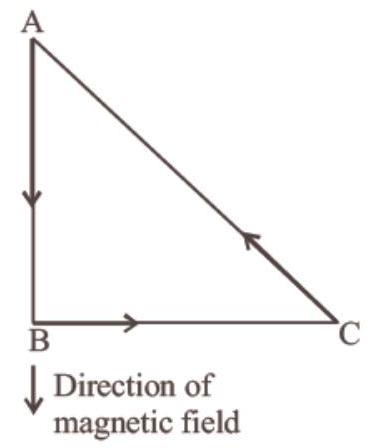
where $B$ is the magnitude of the magnetic force.
The direction of $\vec{F}$ will be in the direction perpendicular to the plane of the paper and going into it.
By Pythagorus theorem,
$AC=\sqrt{x^{2}+x^{2}}=\sqrt{2} x$
$\therefore$ Magnitude of force on AC
$=i \sqrt{2} \times B \sin 45^{\circ}$
$ \begin{aligned} & =i \sqrt{2} x B \times \frac{1}{\sqrt{2}} \\ & =i x B=|\overrightarrow{{}F}| \end{aligned} $
The direction of the force on $A C$ is perpendicular to the plane of the paper and going out of it. Hence, force on $A C=-\vec{F}$










