Moving Charges and Magnetism - Result Question 60
«««< HEAD:content/english/neet-pyq-chapterwise/physics/moving-charges-and-magnetism/moving-charges-and-magnetism-result-question-60.md
61. A rectangular coil of length $0.12 m$ and width 0.1 $m$ having 50 turns of wire is suspended vertically in a uniform magnetic field of strength 0.2 weber/ $m^{2}$. The coil carries a current of $2 A$. If the plane of the coil is inclined at an angle of $30^{\circ}$ with the direction of the field, the torque required to keep the coil in stable equilibrium will be :
======= ####61. A rectangular coil of length $0.12 m$ and width 0.1 $m$ having 50 turns of wire is suspended vertically in a uniform magnetic field of strength 0.2 weber/ $m^{2}$. The coil carries a current of $2 A$. If the plane of the coil is inclined at an angle of $30^{\circ}$ with the direction of the field, the torque required to keep the coil in stable equilibrium will be :
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/moving-charges-and-magnetism/moving-charges-and-magnetism—result-question-60.md (a) $0.20 Nm$
(b) $0.24 Nm$
(c) $0.12 Nm$
(d) $0.15 Nm$
[2015 RS]
Show Answer
Answer:
Correct Answer: 61. (a)
Solution:
- (a) Here, number of turns of coil, $N=50$
Current through the coil $I=2 A$
Area $A=l \times b=0.12 \times 0.1 m^{2}=0.012 m^{2}$
Magnetic field $\vec{B}=0.2 W / m^{2}$
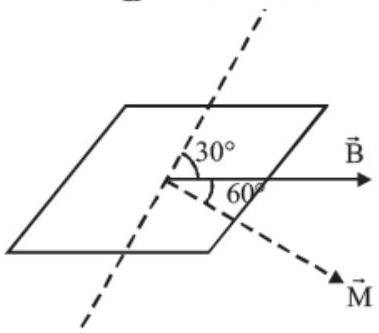
Torque required to keep the coil in stable equilibrium.
$ \begin{aligned} & \tau=\overrightarrow{{}M} \times \overrightarrow{{}B}=MB \sin 60^{\circ}=Ni AB \sin 60^{\circ} \\ & =50 \times 2 \times 0.12 \times 0.1 \times 0.2 \times \frac{\sqrt{3}}{2} \\ & =12 \sqrt{3} \times 10^{-2}=0.20784 Nm \end{aligned} $
magnetic field.










