Moving Charges and Magnetism - Result Question 40
41. A current loop consists of two identical semicircular parts each of radius $R$, one lying in the $x-y$ plane and the other in $x-z$ plane. If the current in the loop is $i$, the resultant magnetic field due to the two semicircular parts at their common centre is
[2010]
(a) $\frac{\mu_0 i}{\sqrt{2} R}$
(b) $\frac{\mu_0 i}{2 \sqrt{2} R}$
(c) $\frac{\mu_0 i}{2 R}$
(d) $\frac{\mu_0 i}{4 R}$
Show Answer
Answer:
Correct Answer: 41. (b)
Solution:
- (b) Magnetic fields due to the two parts at their common centre are respectively, $B_y=\frac{\mu_0 i}{4 R}$ and $B_z=\frac{\mu_0 i}{4 R}$
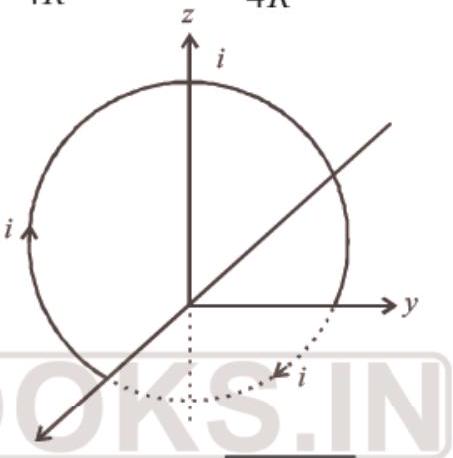
Resultant field $=\sqrt{B_y^{2}+B_z^{2}}$
$={\sqrt{(\frac{\mu_0 i}{4 R})^{2}+(\frac{\mu_0 i}{4 R})}}^{2}=\sqrt{2} \cdot \frac{\mu_0 i}{4 R}=\frac{\mu_0 i}{2 \sqrt{2} R}$










