Moving Charges and Magnetism - Result Question 34
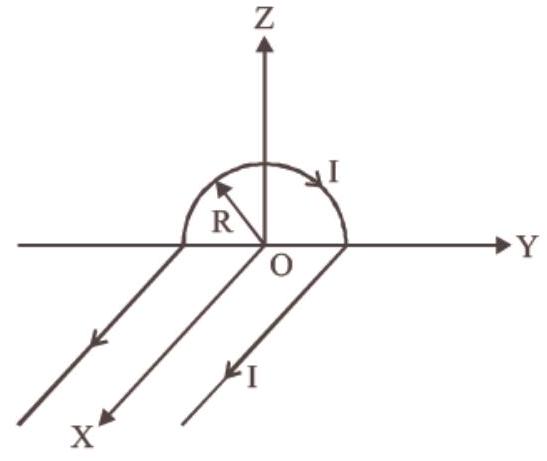
35. A wire carrying current $I$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $X$-axis while semicircular portion of radius $R$ is lying in $Y-Z$ plane. Magnetic field at point $O$ is : [2015]
(a) $\overrightarrow{{}B}=-\frac{\mu_0}{4 \pi} \frac{I}{R}(\mu \hat{i} \times 2 \hat{k})$
(b) $\overrightarrow{{}B}=-\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}+2 \hat{k})$
(c) $\overrightarrow{{}B}=\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}-2 \hat{k})$
(d) $\overrightarrow{{}B}=\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}+2 \hat{k})$
Show Answer
Answer:
Correct Answer: 35. (b)
Solution:
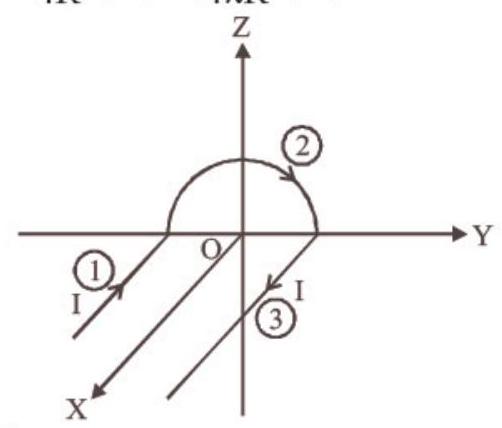
- (b) Magnetic field due to segment ’ 1 '
$ \begin{aligned} & \overrightarrow{{}B_1}=\frac{\mu_0 I}{4 \pi R}\sin 90^{\circ}+\sin 0^{\circ} \\ & =\frac{-\mu_0 I}{4 \pi R}(\hat{k})=\overrightarrow{{}B}_3 \end{aligned} $
Magnetic field due to segment 2
$ B_2=\frac{\mu_0 I}{4 R}(-\hat{i})=\frac{-\mu_0 I}{4 \pi R}(\pi \hat{i}) $
$\therefore \overrightarrow{{}B}$ at centre
$ \overrightarrow{{}B}_c=\overrightarrow{{}B}_1+\overrightarrow{{}B}_2+\overrightarrow{{}B}_3=\frac{-\mu_0 I}{4 \pi R}(\pi \hat{i}+2 \hat{k}) $










