Moving Charges and Magnetism - Result Question 31
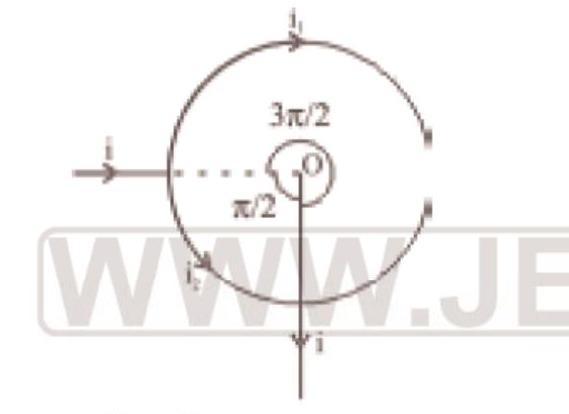
32. A straight conductor carrying current $i$ splits into two parts as shown in the figure. The radius of the circular loop is $R$. The total magnetic field at the centre $P$ of the loop is,
[NEET Odisha 2019]
(a) $\frac{\mu_0 i}{2 R}$, inward
(b) Zero
(c) $3 \mu_0 i / 32 R$, outward
(d) $3 \mu_0 i / 32 R$, inward
Show Answer
Answer:
Correct Answer: 32. (b)
Solution:
- (b) Net magnetic field at point ’ $P$ '
$B _{\text{net }}= \vec{B} _1+ \vec{B} _2$
Hence, $B _{\text{net }}=B_1-B_2$
$i_1=i(\frac{\theta}{2 \pi}) \Rightarrow B_1=\frac{\mu_0 i_1}{2 R}(\frac{2 \pi-\theta}{2 \pi})$
$i_2=i(\frac{2 \pi-\theta}{2 \pi}) \Rightarrow B_2=\frac{\mu_0 i_2}{2 R}(\frac{\theta}{2 \pi})$
Here $\theta=\frac{\pi}{2}$
$B _{\text{net }}=B_1-B_2=0$










