Motion in a Plane - Result Question 49
52. A stone is tied to a string of length $\ell$ and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed $u$. The magnitude of the change in velocity as it reaches a position where the string is horizontal ( $g$ being acceleration due to gravity) is
[2004]
(a) $\sqrt{2 g \ell}$
(b) $\sqrt{2(u^{2}-g \ell)}$
(c) $\sqrt{u^{2}-g \ell}$
(d) $u-\sqrt{u^{2}-2 g \ell}$
Show Answer
Answer:
Correct Answer: 52. (b)
Solution:
- (b) $W _{mg}=\Delta K$
$\Rightarrow-mg \ell=1 / 2 mv^{2}-1 / 2 mu^{2}$
or, $m v^{2}=m(u^{2}-2 g \ell]$
or, $v=\sqrt{u^{2}-2 g \ell} \quad \hat{j}$
$\vec{u}=u \hat{i}$
$\therefore \vec{v}-\vec{u}=\sqrt{u^{2}-2 g \ell} \hat{j}-u \hat{i}$
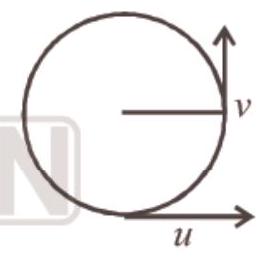
$\therefore|\vec{v}-\vec{u}|=[(u^{2}-2 g \ell)+u^{2}]^{1 / 2}=\sqrt{2(u^{2}-g \ell)}$










