Motion in a Plane - Result Question 40
43. The speed of a swimmer in still water is $20 m /$ s. The speed of river water is $10 m / s$ and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path, the angle at which he should make his strokes w.r.t. north is given by :
[2019]
(a) $30^{\circ}$ west
(b) $0^{\circ}$
(c) $60^{\circ}$ west
(d) $45^{\circ}$ west
Show Answer
Answer:
Correct Answer: 43. (a)
Solution:
- (a) Velocity of swimmer w.r.t. river $V _{S R}=20 m / s$ Velocity of river w.r.t. ground $V _{RG}=10 m / s$
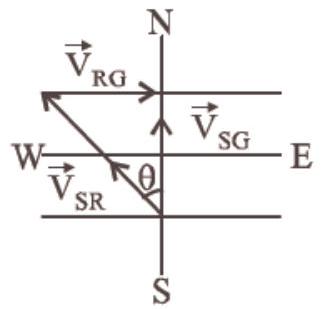
$\overrightarrow{{}V} _{SG}=\overrightarrow{{}V} _{SR}+\overrightarrow{{}V} _{RG}$
$\sin \theta=|\frac{\overrightarrow{{}V} _{RG}}{\overrightarrow{{}V} _{SR}}| \Rightarrow \sin \theta=\frac{10}{20}$
$\Rightarrow \sin \theta=\frac{1}{2} \quad \therefore \theta=30^{\circ}$ west
i.e.,to cross the river along the shortest path, swimmer should make his strokes $30^{\circ}$ west.










