Motion in a Plane - Result Question 34
«««< HEAD:content/english/neet-pyq-chapterwise/physics/motion-in-a-plane/motion-in-a-plane-result-question-34.md
37. A particle of mass $m$ is projected with velocity $v$ making an angle of $45^{\circ}$ with the horizontal. When the particle lands on the level ground the magnitude of the change in its momentum will be:
======= ####37. A particle of mass $m$ is projected with velocity $v$ making an angle of $45^{\circ}$ with the horizontal. When the particle lands on the level ground the magnitude of the change in its momentum will be:
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/motion-in-a-plane/motion-in-a-plane—result-question-34.md (a) $2 mv$
(c) $mv \sqrt{2}$
(b) $mv / \sqrt{2}$
(d) zero
[2008]
Show Answer
Answer:
Correct Answer: 37. (c)
Solution:
- (c) The momentum along $a$-axis remains unchanged
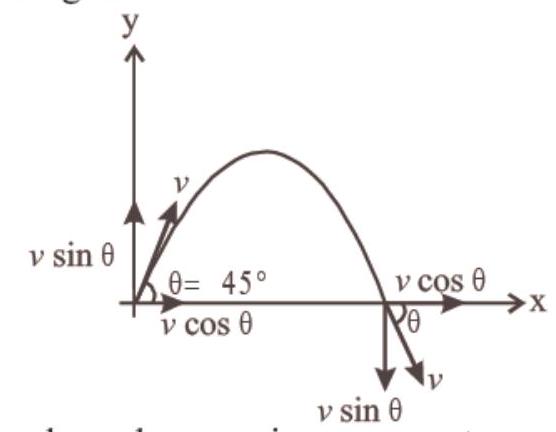
Clearly, change in momentum along $x$-axis $=m v \cos \theta-m v \cos \theta=0$
Momentum changed only in vertical direction or $y$-axis.
$ \begin{aligned} \text{ So, } & \Delta P=\Delta P _{\text{vertical }} \\ \Rightarrow & P _{\text{final }}=P _{\text{initial }} \\ & =m v \sin \theta-(-m v \sin \theta) \\ & =2 m v \sin \theta=2 m v \times \sin 45^{\circ} \\ & =2 m v \times \frac{1}{\sqrt{2}}=\sqrt{2} m v \end{aligned} $
Hence, resultant change in momentum $=\sqrt{2} m v$










