Motion in a Plane - Result Question 26
28. A body of $3 kg$ moves in the $X Y$ plane under the action of a force given by $6 t^{2} \hat{i}+4 t \hat{j}$.
Assuming that the body is at rest at time $t=0$, the velocity of the body at $t=3 s$ is [2002]
(a) $6 \hat{i}+6 \hat{j}$
(b) $18 \hat{i}+6 \hat{j}$
(c) $18 \hat{i}+12 \hat{j}$
(d) $12 \hat{i}+18 \hat{j}$
Show Answer
Solution:
- (b) $\vec{F}=6 t \hat{i}+4 t \hat{j}$
$F_x=6 t, F_y=4 t$
$a_x=\frac{6 t}{3}=2 t, a_y=\frac{4 t}{3}$
$\frac{d v_x}{d t}=2 t^{2}$
$\int_0^{v_x} d V_x=\int_0^{t} 2 t^{2} d t$
$\Rightarrow v_x=\frac{2}{3} t^{3}=\frac{2}{3} \cdot 3^{3}=18$
$ \frac{d V_y}{d t}=\frac{4}{3} t \Rightarrow \int_0^{V_y} d V_y=\frac{4}{3} \int_0^{t} t d t $
$\Rightarrow \quad V_y=\frac{4}{3} \frac{t^{2}}{2}=\frac{4}{3} \cdot \frac{3^{2}}{2}=6$
$\Rightarrow V=18 \vec{t}+6 \vec{T}$
(a) Given, $v_A=10 m / sec$
$ \alpha=60^{\circ} $
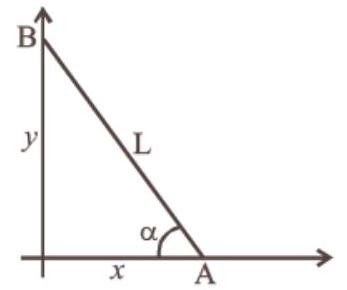
let length of the rod $=L$
From figure,
$\Rightarrow x^{2}+y^{2}=L$
differentiation with respect to time ’ $t$ '
$\Rightarrow 2 x \frac{d x}{d t}+2 y \frac{d y}{d t}=0$
$\Rightarrow x \frac{d x}{d t}+y \frac{d y}{d t}=0$
where, $\frac{d x}{d t}=v_A$ and $\frac{d y}{d t}=v_B$
So, $x v_A+y v_B=0$
$ v_B=\frac{-x}{y} v_A $
where $\frac{x}{y}=\cot \alpha$
So, $v_B=-v_A \cot \alpha$
$ v_B=10 \cot 60^{\circ} $
$ v_B=\frac{-10}{\sqrt{3}}=-5.773 \simeq 5.8 m / sec $










