Motion in a Plane - Result Question 24
«««< HEAD:content/english/neet-pyq-chapterwise/physics/motion-in-a-plane/motion-in-a-plane-result-question-24.md
26. A particle starting from the origin $(0,0)$ moves in the $(x, y)$ plane. Its coordinates at a later time are $(\sqrt{3}, 3)$. The path of the particle makes with the $x$-axis an angle of
======= ####26. A particle starting from the origin $(0,0)$ moves in the $(x, y)$ plane. Its coordinates at a later time are $(\sqrt{3}, 3)$. The path of the particle makes with the $x$-axis an angle of
3e0f7ab6f6a50373c3f2dbda6ca2533482a77bed:content/english/neet-pyq-chapterwise/physics/motion-in-a-plane/motion-in-a-plane—result-question-24.md (a) $45^{\circ}$
(b) $60^{\circ}$
(c) $0^{\circ}$
(d) $30^{\circ}$
[2007]
Show Answer
Answer:
Correct Answer: 26. (b)
Solution:
(b)
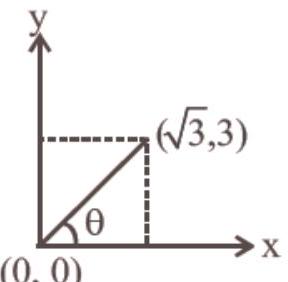
Let $\theta$ be the angle which the particle makes with $x$-axis.
From figure, $\tan \theta=\frac{3}{\sqrt{3}}=\sqrt{3}$
$\Rightarrow \theta=\tan ^{-1}(\sqrt{3})=60^{\circ}$
If a vector $\vec{R}$ in $X-Y$ plane then its orthogonal vector $R_X=R \cos \theta$ and $R_Y=R \sin \theta$.
$ \text{ And } \frac{R \sin \theta}{R \cos \theta}=\tan \theta=\frac{R_Y}{R_X} $










