Mechanical Properties of Solids - Result Question 6
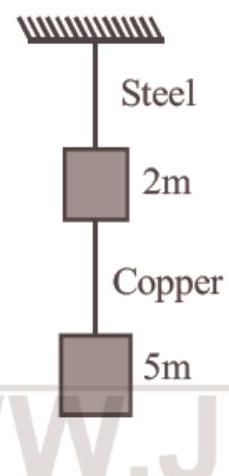
7. If the ratio of diameters, lengths and Young’s modulus of steel and copper wires shown in the figure are $p, q$ and $s$ respectively, then the corresponding ratio of increase in their lengths would be
[NEET Kar: 2013]
(a) $\frac{7 q}{(5 s p)}$
(b) $\frac{5 q}{(7 s p^{2})}$
(c) $\frac{7 q}{(5 s p^{2})}$
(d) $\frac{2 q}{(5 s p)}$
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- (c) From formula,
Increase in length $\quad \Delta L=\frac{F L}{A Y}=\frac{4 F L}{\pi D^{2} Y}$
$ \begin{aligned} \frac{\Delta L_S}{\Delta L_C} & =\frac{F_S}{F_C}(\frac{D_C}{D_S})^{2} \frac{Y_C}{Y_S} \frac{L_S}{L_C}=\frac{7}{5} \times(\frac{1}{p})^{2}(\frac{1}{s}) q \\ & =\frac{7 q}{(5 s p^{2})} \end{aligned} $
If a wire of length $l$ is suspended from a rigid support and $A$ is the area of cross-section of the wire, then mass of the wire, $m=Alp$. Then extension in the wire due to its own weight can be find as follows.
Young Modulus, $Y=\frac{m g}{A} \times \frac{(l / 2)}{\Delta l}$
Here, $L=l / 2$ because the weight of wire acts at the mid point of wire.
$\therefore$ Extension in the wire due to its own weight $\Delta l=\frac{l^{2} p g}{2 Y}$










