Magnetism and Matter - Result Question 4
7. A coil in the shape of an equilateral triangle of side $l$ is suspended between the pole pieces of a permanent magnet such that $\vec{B}$ is in the plane of the coil. If due to a current in the triangle a torque $\tau$ acts on it, the side $l$ of the triangle is
[2005]
(a) $\frac{2}{\sqrt{3}}(\frac{\tau}{B . i})^{\frac{1}{2}}$
(b) $2(\frac{\tau}{\sqrt{3} B . i})^{\frac{1}{2}}$
(c) $\frac{2}{\sqrt{3}}(\frac{\tau}{B . i})$
(d) $\frac{1}{\sqrt{3}} \frac{\tau}{B . i}$
Show Answer
Answer:
Correct Answer: 7. (b)
Solution:
- (b) $\tau=M B \sin \theta$
$\tau=iAB \sin 90^{\circ}$
$\therefore A=\frac{\tau}{i B}$
Also, $A=1 / 2(B C)(A D)$
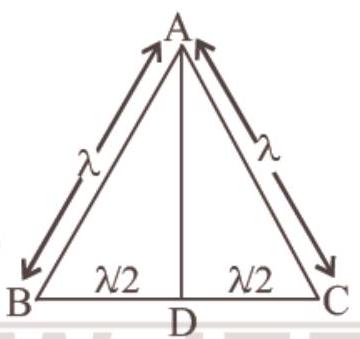
But $\frac{1}{2}(B C)(A D)=\frac{1}{2}(l) \sqrt{l^{2}-(\frac{l}{2})^{2}}$
$=\frac{\sqrt{3}}{4} l^{2} \Rightarrow \frac{\sqrt{3}}{4}(l)^{2}=\frac{\tau}{B i}$
$\therefore \quad l=2(\frac{\tau}{\sqrt{3} B . i})^{\frac{1}{2}}$










