Laws of Motion - Result Question 40
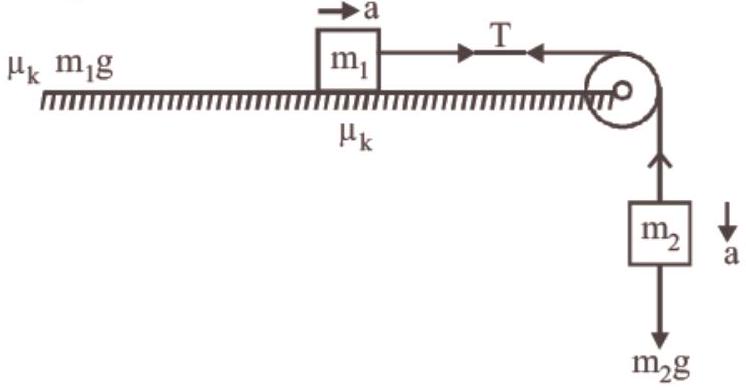
40. A block $A$ of mass $m_1$ rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass $m_2$ is suspended. The coefficient of kinetic friction between the block and the table is $\mu_k$. When the block A is sliding on the table, the tension in the string is
[2015]
(a) $\frac{(m_2-\mu km_1) g}{(m_1+m_2)}$
(b) $\frac{m_1 m_2(1+\mu_k) g}{(m_1+m_2)}$
(c) $\frac{m_1 m_2(1-\mu_k) g}{(m_1+m_2)}$
(d) $\frac{(m_2+\mu_k m_1) g}{(m_1+m_2)}$
Show Answer
Answer:
Correct Answer: 40. (b)
Solution:
- (b) For the motion of both the blocks
$m_1 a=T-\mu_k m_1 g$
$m_2 g-T=m_2 a$
$a=\frac{m_2 g-\mu_k m_1 g}{m_1+m_2}$
$m_2 g-T=(m_2)(\frac{m_2 g-\mu_k m_1 g}{m_1+m_2})$
solving we get tension in the string
$ T=\frac{m_1 m_2 g(1+\mu_k) g}{m_1+m_2} $










