Laws of Motion - Result Question 23
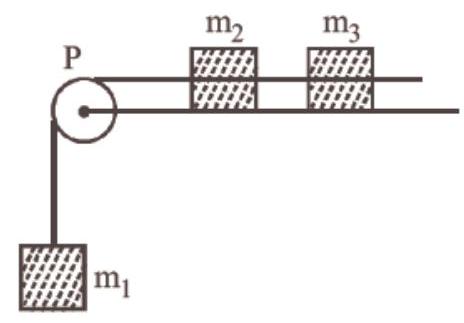
23. A system consists of three masses $m_1, m_2$ and $m_3$ connected by a string passing over a pulley P. The mass $m_1$ hangs freely and $m_2$ and $m_3$ are on a rough horizontal table (the coefficient of friction $=\mu$ ). The pulley is frictionless and of negligible mass. The downward acceleration of mass $m_1$ is : $(.$ Assume $.m_1=m_2=m_3=m)$
[2014]
(a) $\frac{g(1-g \mu)}{g}$
(b) $\frac{2 g \mu}{3}$
(c) $\frac{g(1-2 \mu)}{3}$
(d) $\frac{g(1-2 \mu)}{2}$
Show Answer
Answer:
Correct Answer: 23. (c)
Solution:
- (c) Acceleration
$=\frac{\text{ Net force in the direction of motion }}{\text{ Total mass of system }}$
$ \begin{aligned} &=\frac{m_1 g-\mu(m_2+m_3) g}{(m_1+m_2+m_3)}=\frac{g}{3}(1-2 \mu) \\ &(\because m_1..=m_2=m_3=m \text{ given }) \end{aligned} $










