Electrostatic Potential and Capacitance - Result Question 7
8. Four point charges $-Q,-q, 2 q$ and $2 Q$ are placed, one at each corner of the square. The relation between $Q$ and $q$ for which the potential at the centre of the square is zero is :
[2012]
(a) $Q=-q$
(b) $Q=-\frac{1}{q}$
(c) $Q=q$
(d) $Q=\frac{1}{q}$
Show Answer
Answer:
Correct Answer: 8. (a)
Solution:
- (a) Let the side length of square be ’ $a$ ’ then potential at centre $O$ is
$ \begin{aligned} & A C=B D=\sqrt{a^{2}+a^{2}}=a \sqrt{2} \\ & O A=O B=O C=O D=\frac{a \sqrt{2}}{2}=\frac{a}{\sqrt{2}} \end{aligned} $
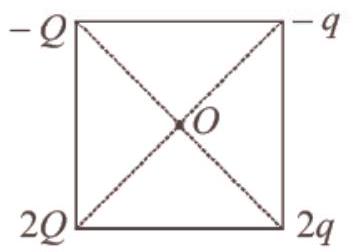
$ \begin{aligned} V & =\frac{k(-Q)}{(\frac{a}{\sqrt{2}})}+\frac{k(-q)}{\frac{a}{\sqrt{2}}}+\frac{k(2 q)}{\frac{a}{\sqrt{2}}}+\frac{k(2 Q)}{\frac{a}{\sqrt{2}}}=0 \\ & =-Q-q+2 q+2 Q=0 \Rightarrow Q+q=0 \\ & \Rightarrow Q=-q \end{aligned} $










