Electrostatic Potential and Capacitance - Result Question 26
28.
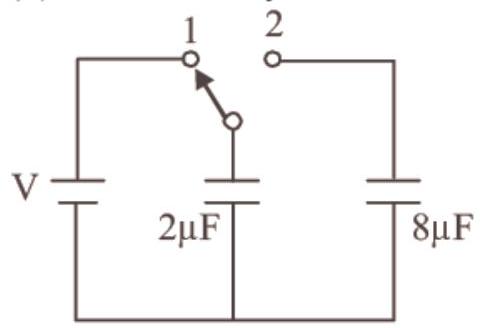
A capacitor of $2 \mu F$ is charged as shown in the diagram. When the switch $S$ is turned to position 2 , the percentage of its stored energy dissipated is :
(a) $0 %$
(b) $20 %$
(c) $75 %$
(d) $80 %$
[2016]
Show Answer
Answer:
Correct Answer: 28. (d)
Solution:
- (d) When $S$ and 1 are connected
The $2 \mu F$ capacitor gets charged. The potential difference across its plates will be $V$.
The potential energy stored in $2 \mu F$ capacitor
$U_i=\frac{1}{2} C V^{2}=\frac{1}{2} \times 2 \times V^{2}=V^{2}$
When $S$ and 2 are connected
The $8 \mu F$ capacitor also gets charged. During this charging process current flows in the wire and some amount of energy is dissipated as heat. The energy loss is
$ \Delta U=\frac{1}{2} \frac{C_1 C_2}{C_1+C_2}(V_1-V_2)^{2} $
Here, $C_1=2 \mu F, C_2=8 \mu F, V_1=V, V_2=0$
$\therefore \Delta U=\frac{1}{2} \times \frac{2 \times 8}{2+8}(V-0)^{2}=\frac{4}{5} V^{2}$
The percentage of the energy dissipated
$ =\frac{\Delta U}{U_i} \times 100=\frac{\frac{4}{5} V^{2}}{V^{2}} \times 100=80 % $










