Electrostatic Potential and Capacitance - Result Question 17
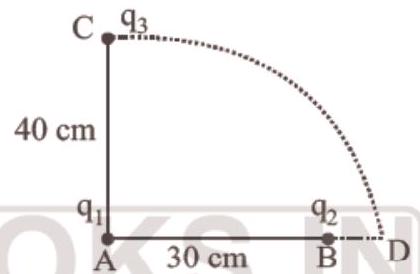
19. Two charges $q_1$ and $q_2$ are placed $30 cm$ apart, as shown in the figure. A third charge $q_3$ is moved along the arc of a circle of radius $40 cm$ from $C$ to $D$. The change in the potential energy of the system is $\frac{q_3}{4 \pi \epsilon_0} k$, where $k$ is
[2005]
(a) $8 q_1$
(b) $6 q_1$
(c) $8 q_2$
(d) $6 q_2$
Show Answer
Answer:
Correct Answer: 19. (c)
Solution:
- (c) We know that potential energy of discrete system of charges is given by
$U=\frac{1}{4 \pi \epsilon_0}(\frac{q_1 q_2}{r _{12}}+\frac{q_2 q_3}{r _{23}}+\frac{q_3 q_1}{r _{31}})$
Here, $r _{12}=A B=0.3 m, r _{31}=A C=0.4 m$
According to question,
$ \begin{aligned} U _{\text{initial }} & =\frac{1}{4 \pi \epsilon_0}(\frac{q_1 q_2}{0.3}+\frac{q_2 q_3}{0.5}+\frac{q_3 q_1}{0.4}) \\ r _{23} & =\sqrt{(0.3)^{2}+(0.4)^{2}}=0.5 m \end{aligned} $
When the charge moved to point $D$
$r _{12}=0.3 m$
$r _{23}=0.1 m$
$r _{31}=0.4 m$
$U _{\text{final }}=\frac{1}{4 \pi \epsilon_0}(\frac{q_1 q_2}{0.3}+\frac{q_2 q_3}{0.1}+\frac{q_3 q_1}{0.4})$
$U _{\text{final }}-U _{\text{initial }}=\frac{1}{4 \pi \epsilon_0}(\frac{q_1 q_2}{0.1}-\frac{q_2 q_3}{0.5})$
$=\frac{1}{4 \pi \epsilon_0}[10 q_2 q_3-2 q_2 q_3]=\frac{q_3}{4 \pi \epsilon_0}(8 q_2)$
When we use the formula of potential energy of system of charges, then we consider that potential energy of the system at infinity is zero.










