Electric Charges and Fields - Result Question 5
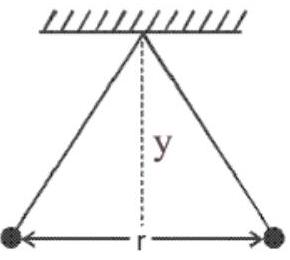
5. Two pith balls carrying equal charges are suspended from a common point by strings of equal length. The equilibrium separation between them is $r$. Now the strings are rigidly
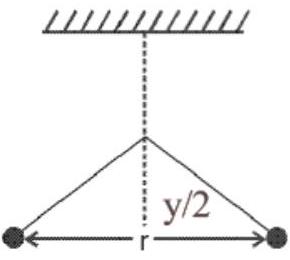
clamped at half the height. The equilibrium separation between the balls now become
[2013]
(a) $(\frac{r}{\sqrt[3]{2}})$
(c) $(\frac{2 r}{3})$ (b) $(\frac{2 r}{\sqrt{3}})$
(d) $(\frac{r}{\sqrt{2}})^{2}$
Show Answer
Answer:
Correct Answer: 5. (a)
Solution:
- (a)
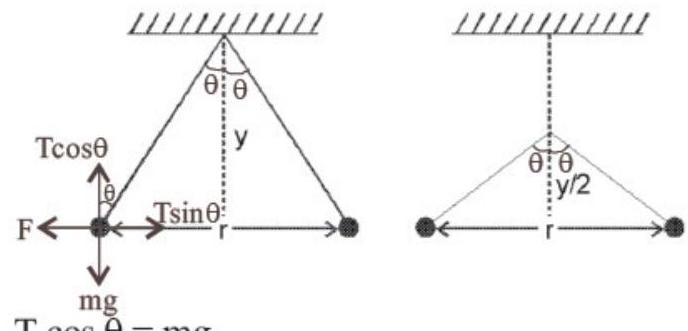
$T \cos \theta=mg$
$T \sin \theta=F$
$\therefore \quad \tan \theta=\frac{F}{mg}$
From figure, $\tan \theta=\frac{F_e}{m g}$
$\Rightarrow \frac{r / 2}{y}=\frac{\frac{kq^{2}}{r^{2}}}{mg}$
$[\because F=\frac{kq^{2}}{r^{2}}.$ from coulomb’s law] $\Rightarrow r^{3} \propto y$
When string is clamped at half the height $r^{\prime 3} \propto \frac{y}{2}$
Dividing the above two equations, we have $\frac{r^{\prime}}{r}=\frac{1}{2^{1 / 3}} \Rightarrow r^{\prime}=\frac{r}{\sqrt[3]{2}}$










