Electric Charges and Fields - Result Question 4
4. Two identical charged spheres suspended from a common point by two massless strings of lengths $l$, are initially at a distance $d(d«l)$ apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity $v$. Then $v$ varies as a function of the distance x between the spheres, as :
[2016]
(a) $v \propto x^{\frac{1}{2}}$
(b) $v \propto x$
(c) $v \propto x^{-\frac{1}{2}}$
(d) $v \propto x^{-1}$
Show Answer
Answer:
Correct Answer: 4. (c)
Solution:
- (c) From figure $T \cos \theta=mg$
$T \sin \theta=\frac{kq^{2}}{x^{2}}$
so, $\tan \theta=\frac{F_e}{mg} \simeq \theta$
$ \tan \theta=\frac{kq^{2}}{x^{2} mg} $
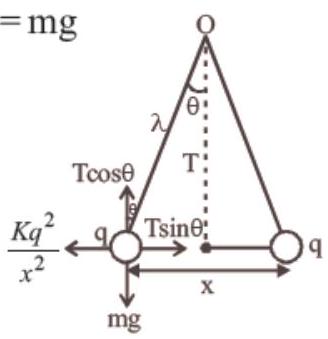
As $\theta$ is $small \tan \theta \approx \sin \theta=\frac{x}{2 l}$
$\therefore \quad \frac{kq^{2}}{x^{2} mg}=\frac{x}{2 \ell}$
or $x^{3} \propto q^{2}$
or $x^{3 / 2} \propto q$
Differentiating eq. (1) w.r.t. time
$3 x^{2} \frac{dx}{dt} \propto 2 q \frac{dq}{dt}$ but $\frac{dq}{dt}$ is constant
so $x^{2}(v) \propto q$
Replace q from eq. (2)
$x^{2}(v) \propto x^{3 / 2}$ or $v \propto x^{-1 / 2}$










