Electric Charges and Fields - Result Question 14
14. A hollow metal sphere of radius $R$ is uniformly charged. The electric field due to the sphere at a distance $r$ from the centre :
[2019]
(a) increases as $r$ increases for $r<R$ and for $r>R$
(b) zero as $r$ increases for $r<R$, decreases as $r$ increases for $r>R$
(c) zero as $r$ increases for $r<R$, increases as $r$ increases for $r>R$
(d) decreases as $r$ increases for $r<R$ and for $r>R$
Show Answer
Answer:
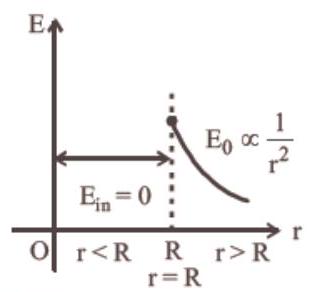
Correct Answer: 14. (b)
Solution:
(b) Charge $Q$ will be distributed over the surface of hollow metal sphere.
(i) For $r<R$ (inside)
[At a point inside the hollow sphere]
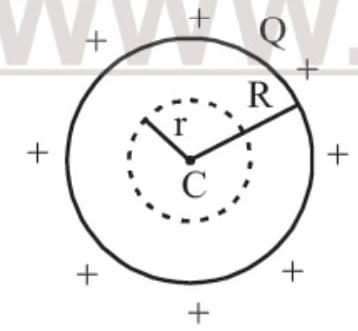
By Gauss’s law, $\oint \overrightarrow{{}E} _{in} \cdot \overrightarrow{{}dS}=\frac{q _{en}}{\varepsilon_0}=0$
As enclosed charge is $=0$
So, $E _{\text{in }}=0$ the electric field inside the hollow sphere is always zero.
(ii) For $r>R$ (outside)
[At a point outside hollow sphere]
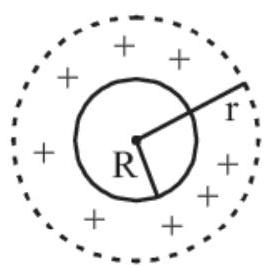
By Gauss’s law, $\oint \overrightarrow{{}E}_0 \cdot \overrightarrow{{}dS}=\frac{q _{en}}{\varepsilon_0} \quad(Q q _{en}=Q)$
$ \begin{aligned} & \therefore E_0 4 \pi r^{2}=\frac{Q}{\varepsilon_0} \\ & \therefore E_0 \propto \frac{1}{r^{2}} \end{aligned} $