Current Electricity - Result Question 89
94. A resistance wire connected in the left gap of a metre bridge balances a $10 \Omega$ resistance in the right gap at a point which divides the bridge wire in the ratio $3: 2$. If the length of the resistance wire is $1.5 m$, then the length of $1 \Omega$ of the resistance wire is :
[2020]
(a) $1.0 \times 10^{-1} m$
(b) $1.5 \times 10^{-1} m$
(c) $1.5 \times 10^{-2} m$
(d) $1.0 \times 10^{-2} m$
Show Answer
Answer:
Correct Answer: 94. (a)
Solution:
- (a) Let $R_1$ be the resistance of resistance wire.
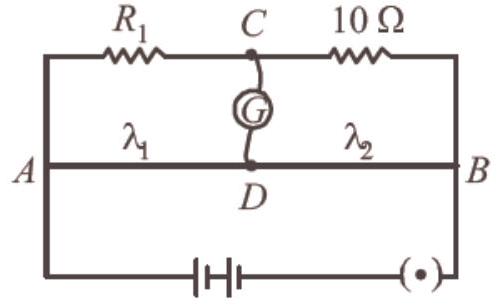
From the balancing condition of metre bridge,
$ \frac{R_1}{10}=\frac{\ell_1}{\ell_2}=\frac{3}{2} \Rightarrow R_1=\frac{30}{2}=15 \Omega $
Length of $15 \Omega$ resistance wire is $1.5 m$.
$\therefore$ Length of $1 \Omega$ resistance wire
$=\frac{1.5}{15}=0.1 m=1.0 \times 10^{-1} m$










