Current Electricity - Result Question 67
72. The power dissipated in the circuit shown in the figure is 30 Watts. The value of $R$ is: [2012M]
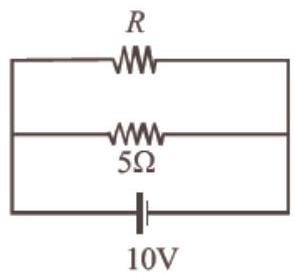
(a) $20 \Omega$
(b) $15 \Omega$
(c) $10 \Omega$
(d) $30 \Omega$
Show Answer
Answer:
Correct Answer: 72. (c)
Solution:
- (c) The power dissipated in the circuit.
$P=\frac{V^{2}}{R _{eq}}$
$V=10$ volt
$\frac{1}{R _{eq}}=\frac{1}{R}+\frac{1}{5}=\frac{5+R}{5 R}$
$R _{eq}=(\frac{5 R}{5+R})$
$P=30 W$
Substituting the values in equation (i)
$30=\frac{(10)^{2}}{(\frac{5 R}{5+R})}$
$\frac{15 R}{5+R}=10$
$15 R=50+10 R$
$5 R=50$
$R=10 \Omega$
For a given voltage $V$, if resistance is changed from $R$ to $(\frac{R}{n})$. Power consumed changes from $P$ to $n P$.
$P=\frac{V^{2}}{R}$
when $R^{\prime}=\frac{R}{n}$
then $P^{\prime}=\frac{V^{2}}{R / n}=\frac{n V^{2}}{R}=n P$










