Current Electricity - Result Question 63
67. Six similar bulbs are connected as shown in the figure with a DC source of emf E, and zero internal resistance.
The ratio of power consumption by the bulbs when (i) all are glowing and (ii) in the situation when two from section $A$ and one from section $B$ are
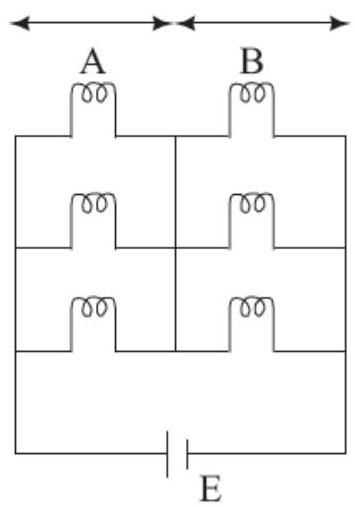glowing, will be:
(a) $4: 9$
(b) $9: 4$
(c) $1: 2$
(d) $2: 1$
[2019]
Show Answer
Answer:
Correct Answer: 67. (b)
Solution:
- (b) When all bulbs are glowing
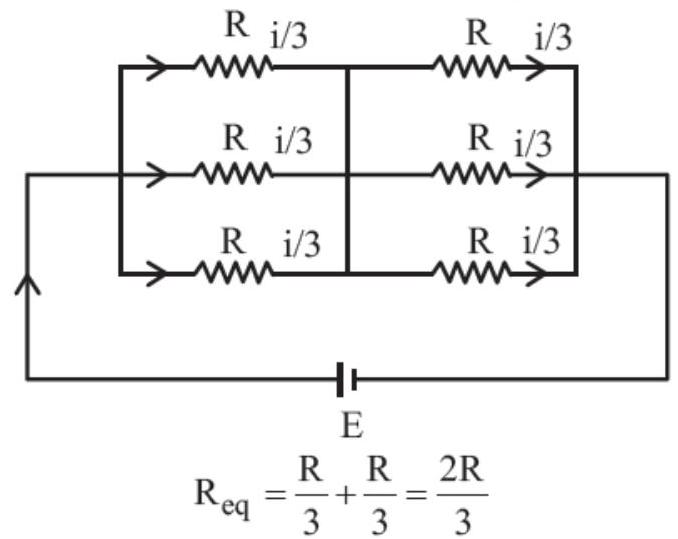
Power $(P_i)=\frac{E^{2}}{R _{\text{eq }}}=\frac{3 E^{2}}{2 R}$
When two from section $A$ and one from section $B$ are glowing, then
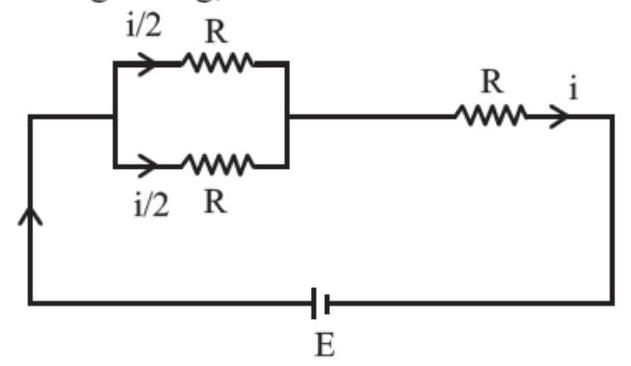
$R _{\text{eq }}=\frac{R}{2}+R=\frac{3 R}{2}$
Power $(P_f)=\frac{2 E^{2}}{3 R}$
Dividing equation (i) by (ii) we get
$\frac{P_i}{P_f}=\frac{3 E^{2} 3 R}{2 R 2 E^{2}}=9: 4$
(a) Given: Charge $Q=at-bt^{2}$
$\therefore$ Current $i=\frac{\partial Q}{\partial t}=a-2 bt$
$ {\text{ for } i=0 \Rightarrow t=\frac{a}{2 b}} $
From joule’s law of heating, heat produced $dH=i^{2} Rdt$
$H=\int_0^{a / 2 b}(a-2 b t)^{2} R d t$
$H=.\frac{(a-2 b t)^{3} R}{-3 \times 2 b}|_0 ^{\frac{a}{2 b}}=\frac{a^{3} R}{6 b}$
