Current Electricity - Result Question 26
27. A ring is made of a wire having a resistance $R_0=12 \Omega$. Find the points $A$ and $B$ as shown in the figure, at which a current carrying conductor should be connected so that the resistance $R$ of the sub-circuit between these points is equal
to $\frac{8}{3} \Omega$.
[2012]
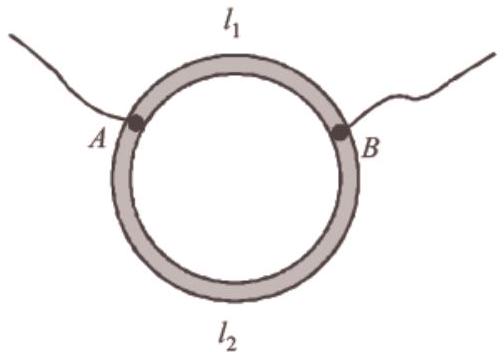
(a) $\frac{l_1}{l_2}=\frac{5}{8}$
(b) $\frac{l_1}{l_2}=\frac{1}{3}$
(c) $\frac{l_1}{l_2}=\frac{3}{8}$
(d) $\frac{l_1}{l_2}=\frac{1}{2}$
Show Answer
Answer:
Correct Answer: 27. (d)
Solution:
- (d) Let $x$ is the resistance per unit length then
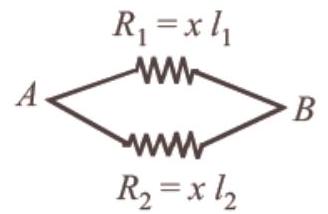
equivalent resistance $R=\frac{R_1 R_2}{R_1+R_2} \frac{(x l_1)(x l_2)}{x l_1+x l_2}$
$ \begin{align*} & \Rightarrow \frac{8}{3}=x \frac{l_1 l_2}{l_1+l_2} \\ & \frac{8}{3}=x \frac{l_1}{\frac{l_1}{l_2}+1} \tag{i} \end{align*} $
also $R_0=x l_1+x l_2$
$ 12=x(l_1+l_2) $
$ \begin{equation*} 12=x l_2(\frac{l_1}{l_2}+1) \tag{ii} \end{equation*} $
Resistances of complete circle/wire $=12 \times 0.2 \pi$ $=2.4 \pi \Omega$
$\therefore$ Resistance of each semi-circle $=1.2 \pi \Omega$
Hence, equivalent resistance,










