Alternating Current - Result Question 27
27. In a circuit, $L, C$ and $R$ are connected in series with an alternating voltage source of frequency f. The current leads the voltage by $45^{\circ}$. The value of $C$ is
[2005]
(a) $\frac{1}{\pi f(2 \pi f L-R)}$
(b) $\frac{1}{2 \pi f(2 \pi f L-R)}$
(c) $\frac{1}{\pi f(2 \pi f L+R)}$
(d) $\frac{1}{2 \pi f(2 \pi f L+R)}$
Show Answer
Answer:
Correct Answer: 27. (d)
Solution:
- (d) From figure,
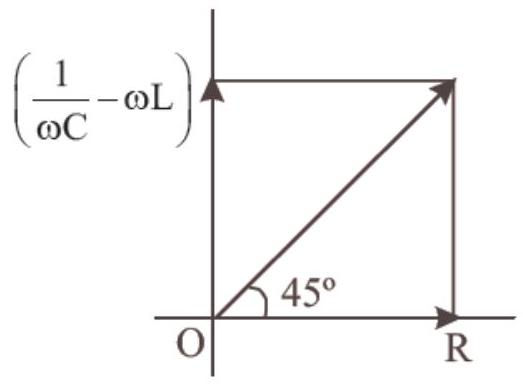
$\tan 45^{\circ}=\frac{\frac{1}{\omega C}-\omega L}{R} \Rightarrow \frac{1}{\omega C}-\omega L=R$
$\Rightarrow \frac{1}{\omega C}=R+\omega L \quad(Q \omega=\frac{2 \pi}{T}=2 \mu f)$
$C=\frac{1}{\omega(R+\omega L)}=\frac{1}{2 \pi f(R+2 \pi f L)}$










