Thermodynamics and Thermochemistry 1 Question 65
68. Two moles of a perfect gas undergo the following processes :
(a) a reversible isobaric expansion from $(1.0 \mathrm{~atm}, 20.0 \mathrm{~L})$ to $(1.0 \mathrm{~atm}, 40.0 \mathrm{~L})$ (b) a reversible isochoric change of state from $(1.0 \mathrm{~atm}$, $40.0 \mathrm{~L})$ to $(0.5 \mathrm{~atm}, 40.0 \mathrm{~L})$
(c) a reversible isothermal compression from $(0.5 \mathrm{~atm}$, $40.0 \mathrm{~L})$ to ( $1.0 \mathrm{~atm}, 20.0 \mathrm{~L})$
(i) Sketch with labels each of the processes on the same $p$ - $V$ diagram.
(ii) Calculate the total work $(W)$ and the total heat change $(Q)$ involved in the above processes.
(iii) What will be the values of $\Delta U, \Delta H$ and $\Delta S$ for the overall process?
(2002, 5M)
Show Answer
Solution:
- (i)
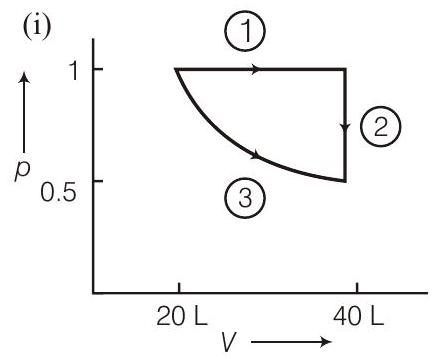
$$ \begin{aligned} -W_{1} & =p \Delta V=20 \mathrm{~L} \text { atm } \ W_{2} & =0 \quad \because \quad \Delta V=0 \ W_{3} & =n R T \ln \frac{40}{20}=20 \ln 2 \end{aligned} $$
Total work done $=W_{1}+W_{2}+W_{3}$
$$ \begin{aligned} & =-20 \mathrm{~L} \mathrm{~atm}+0+20 \ln 2 \ & =-6.14 \mathrm{~atm} \end{aligned} $$
From first law : $q=\Delta E+(-W)=-W$
$$ \Rightarrow \quad q=6.14 \mathrm{~L} \mathrm{~atm}=622.53 \mathrm{~J} $$
(iii) All the states function, $\Delta U, \Delta H$ and $\Delta S$ are zero for cyclic process.










