Thermodynamics and Thermochemistry 1 Question 51
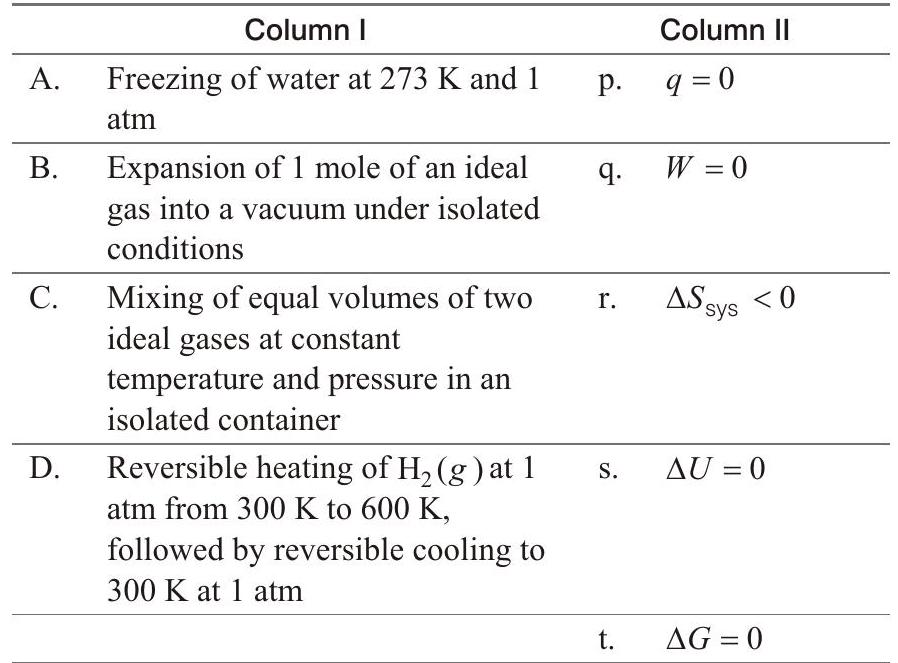
54. Match the thermodynamic processes given under Column I with the expressions given under Column II.
Show Answer
Solution:
- (A) $\rightarrow \mathrm{r}, \mathrm{t}$; (B) $\rightarrow \mathrm{p}, \mathrm{q}, \mathrm{s}$; (C) $\rightarrow \mathrm{p}, \mathrm{q}, \mathrm{s} ;(\mathrm{D}) \rightarrow \mathrm{q}, \mathrm{s}, \mathrm{t}$
(A) $\mathrm{H}{2} \mathrm{O}(l) \underset{1 \text { atm }}{\stackrel{0^{\circ} \mathrm{C}}{\rightleftharpoons}} \mathrm{H}{2} \mathrm{O}(s)$
$q<0, W<0$ (expansion)
$\Delta S_{\text {sys }}<0$ (solid state is more ordered than liquid state)
$\Delta U<0 ; \Delta G=0$ (At equilibrium)
(B) $q=0$ (isolated), $W=0\left(p_{\text {ext }}=0\right)$
$\Delta \mathrm{S}{\text {sys }}>0 \quad \because V{2}>V_{1}$
$\Delta U=0 \because q=W=0$
$\Delta G<0 \because p_{2}<p_{1}$
(C) $q=0$ (isothermal mixing of ideal gases at constant $p$ )
$W=0 \because \Delta U=0 ; q=0, \Delta S_{\text {sys }}>0$
$\because V_{2}>V_{1}, \Delta U=0$
$\because \Delta T=0$
$\Delta G<0 \because$ mixing is spontaneous.
(D) $q=0$ (returning to same state and by same path)
$$ W=0 $$
$\Delta S_{\text {sys }}=0$ (same initial and final states)
$\Delta U=0$
$\because T_{i}=T_{f}, \Delta G=0$










