Thermodynamics and Thermochemistry 1 Question 41
44. The reversible expansion ob an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is (are) correct?
(2012)
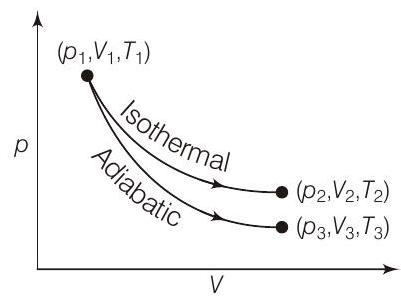
(a) $T_{1}=T_{2}$
(b) $T_{3}>T_{1}$
(c) $W_{\text {isothermal }}>W_{\text {adiabatic }}$
(d) $\Delta U_{\text {isothermal }}>\Delta U_{\text {adiabatic }}$
Show Answer
Solution:
- (a) Since, change of state $\left(p_{1}, V_{1}, T_{1}\right)$ to $\left(p_{2}, V_{2}, T_{2}\right)$ is isothermal therefore, $T_{1}=T_{2}$.
(b) Since, change of state $\left(p_{1}, V_{1}, T_{1}\right)$ to $\left(p_{3}, V_{3}, T_{3}\right)$ is an adiabatic expansion it brings about cooling of gas, therefore, $T_{3}<T_{1}$.
(c) Work done is the area under the curve of $p-V$ diagram. As obvious from the given diagram, magnitude of area under the isothermal curve is greater than the same under adiabatic curve, hence $W_{\text {isothermal }}>W_{\text {adiabatic }}$
(d) $\Delta U=n C_{v} \Delta T$
In isothermal process, $\Delta U=0$ as $\Delta T=0$
In adiabatic process, $\Delta U=n C_{v}\left(T_{3}-T_{1}\right)<0$ as $T_{3}<T_{1}$.
$$ \Rightarrow \quad \Delta U_{\text {isothermal }}>\Delta U_{\text {adiabatic }} $$
NOTE Here only magnitudes of work is being considered otherwise both works have negative sign.










